Rで試す中心極限定理

統計の表現になれのない人のために、表現について少し解説を加えておく。ここでは、正規分布ではない確率分布として、ポアソン分布を例に挙げようと思う。確率変数¹がある確率分布に従うとき、それはニョロニョロ（Tilde, ～）をつかって表現される。例えば、確率変数Xが平均２のポアソン分布に従う場合、次のように書く：

\[ X \sim \text{Poisson}(2) \]

試しにRでXを生成してみる（rpois()はポアソン分布に従う乱数を生成）。

# produce 3 samples of X that follows a Poisson distribution with a mean 2
(X <- rpois(n = 3, lambda = 2))

## [1] 1 2 2

この例では、３サンプル生成してみると、1, 2, 2 となった。ここで、最初の文言に戻ってみよう。

「サンプルサイズ（標本数）が増えれば、どんな確率変数も正規分布で近似できる」

この言葉を字面通りに受け取ると、サンプルをどんどん増やしていけばXはいずれ正規分布に近づくように解釈できる。もしそうならば、サンプル数を増やすほど、Xの頻度分布はきれいな左右対称の鐘状になるはずだ。試してみよう。まずは100サンプル。

# histogram with 100 samples
X <- rpois(n = 100, lambda = 2)
plot(table(X))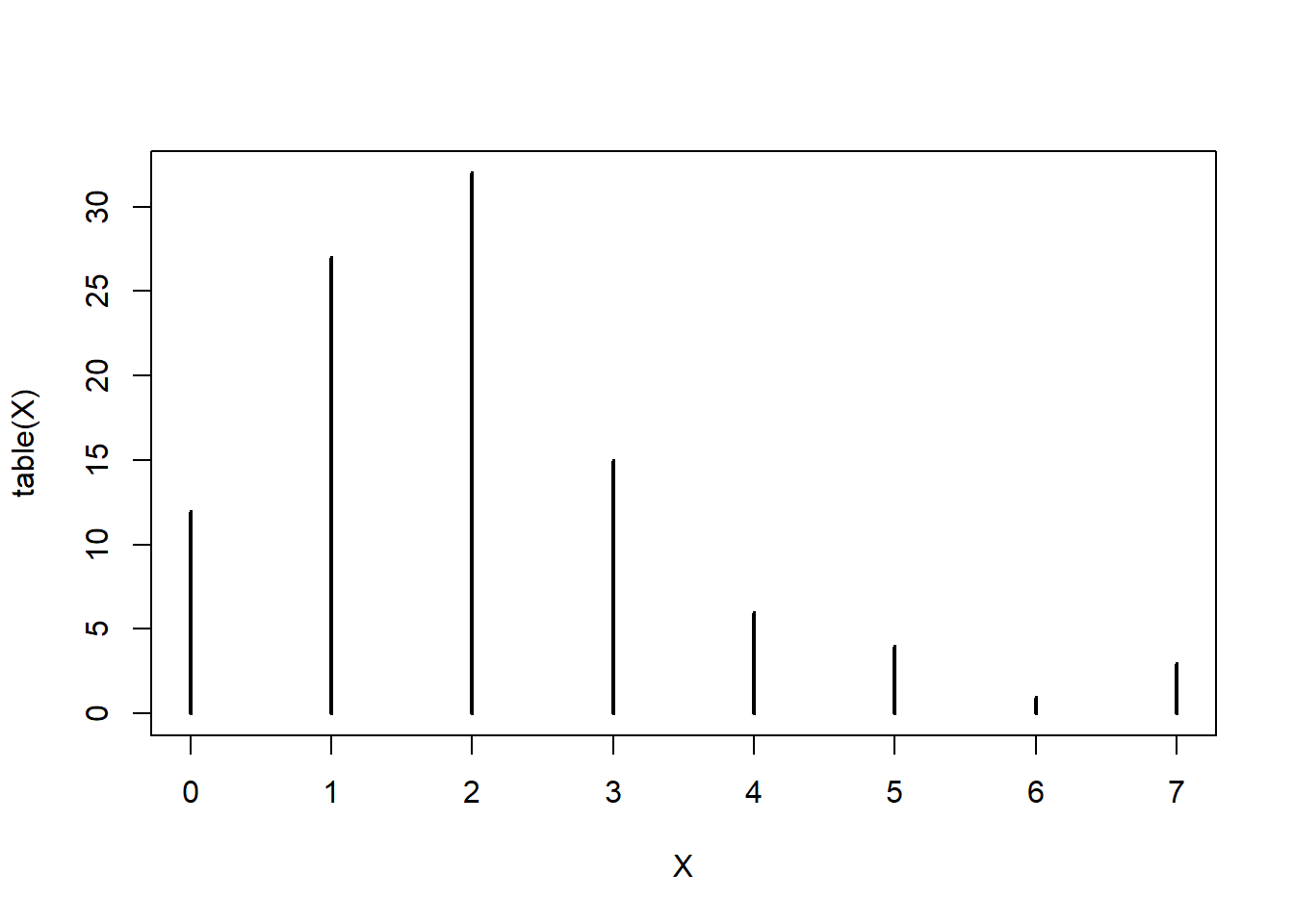

うーん、歪んでいる。１万ならどうだ。

# histogram with 10000 samples
X <- rpois(n = 10000, lambda = 2)
plot(table(X))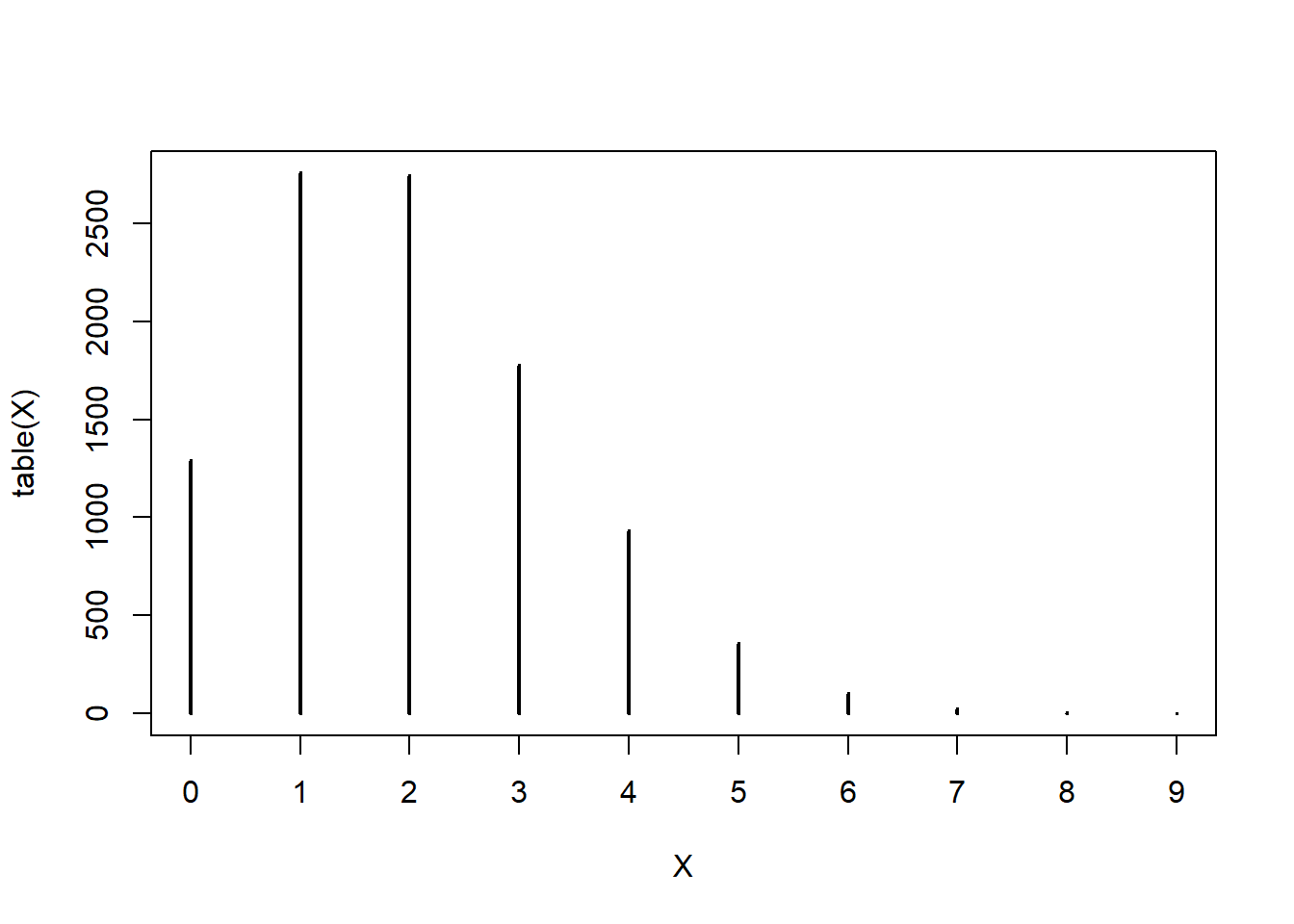

そろそろわかると思うが、Xのサンプルサイズを増やしたところでXはポアソン分布のままである。そう、中心極限定理は、そもそもこんなことは言っていないので当然である。

実際の答えはこうだ：

「ある確率分布に従う確率変数Ｘがある。複数のＸを足し合わせた新たな確率変数Ｙ（\(Y = \sum_i X_i\)）を考える²。この時、足し合わせるＸの個数が多ければ、Ｙは漸近的に正規分布に従う 」

Rで試してみよう。100個のXを足した値をYとして、それを1000個生成する。

## Take a sum of 100 poisson samples for 1000 times
Y <- replicate(1000,
               sum(rpois(100, lambda = 2)))

plot(table(Y))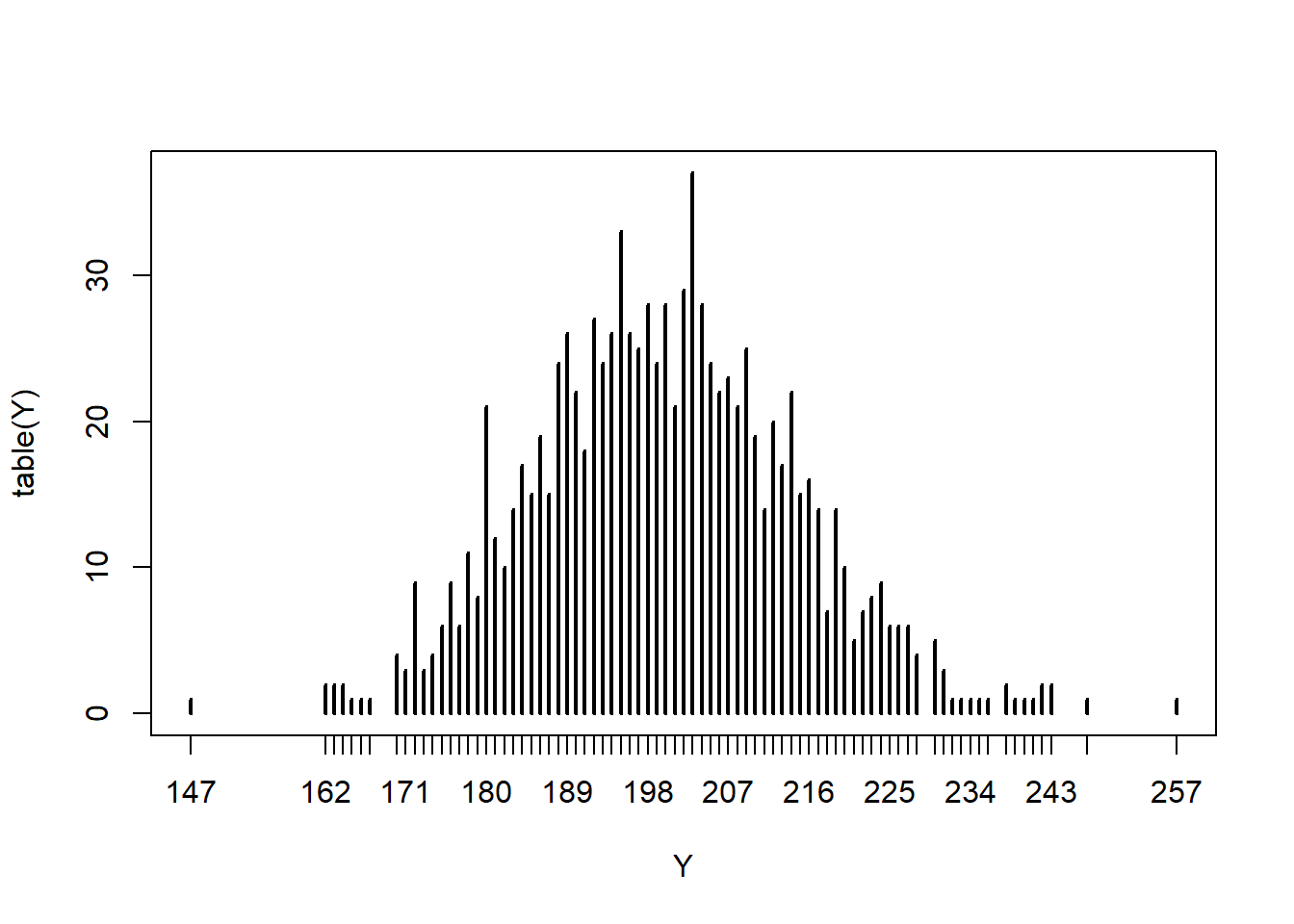

おお、ちゃんと正規分布っぽくなった³。和ではなく、平均をとってもよい（そもそも、和と平均は統計的な意味合いは同じ）。こちらも試してみる。

## Take a mean of 100 poisson samples for 1000 times
Y <- replicate(1000,
               mean(rpois(100, lambda = 2)))

plot(table(Y))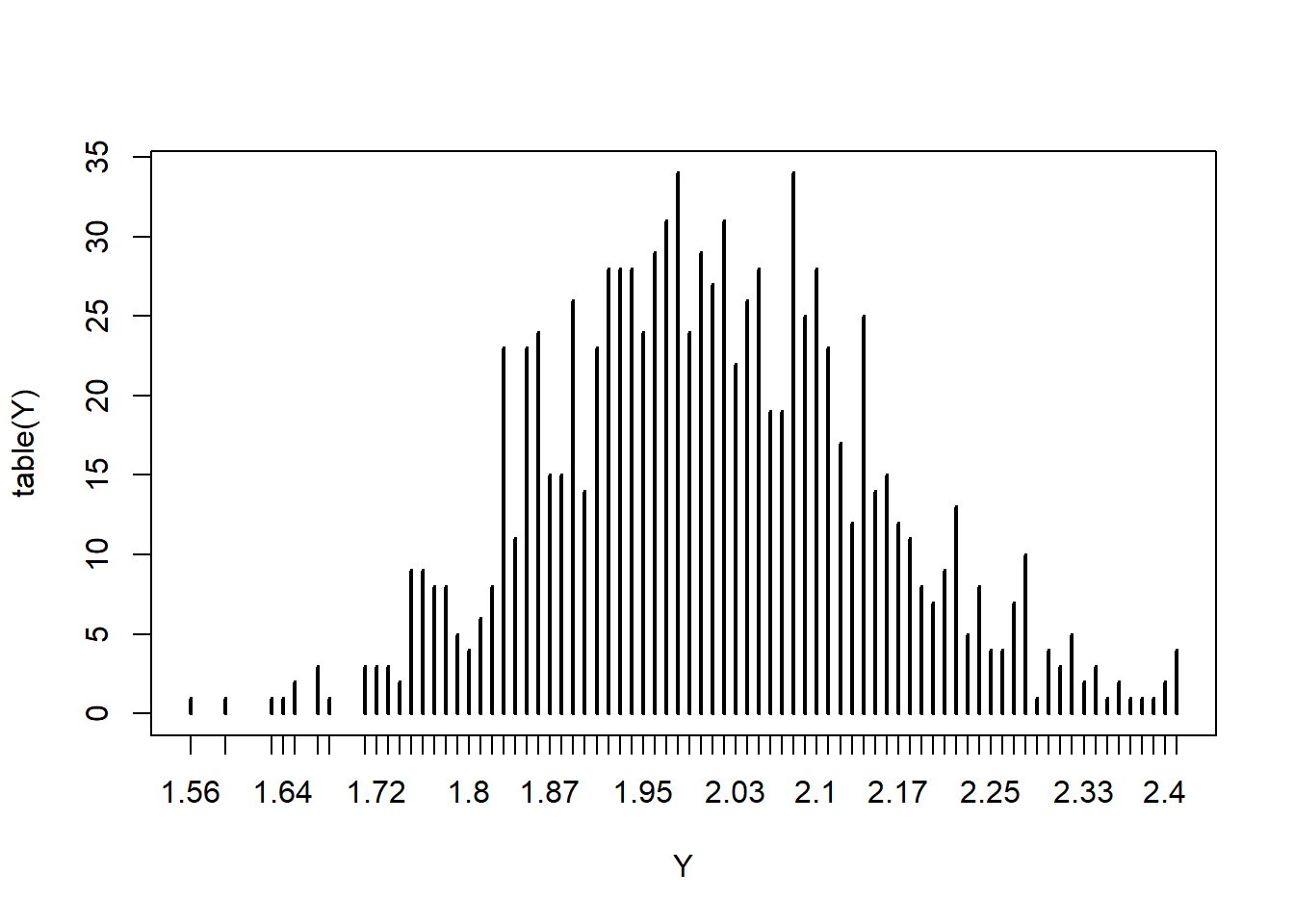

中心極限定理のすごいところは、確率変数\(X\)の確率分布によらず、この定理が成り立つ点にある。例えば、平均2の幾何分布を考えてみる。元の分布は正規分布からほど遠い。

# geometric distribution with mean of 2 (mean = 1 / prob)
X <- rgeom(n = 10000, prob = 0.5)
plot(table(X))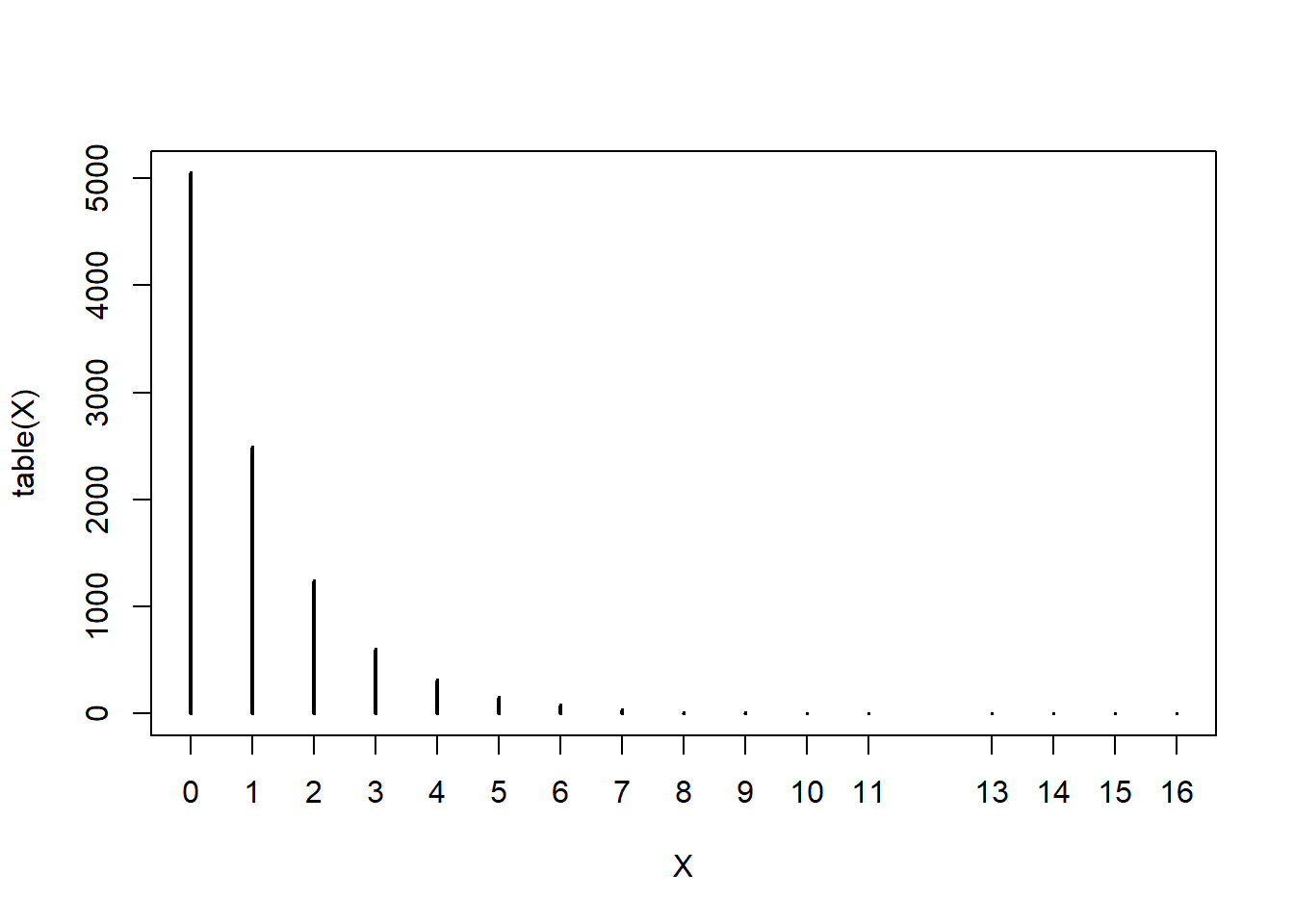

足し合わせて、Yの分布を見てみる。

Y <- replicate(1000,
               sum(rgeom(100, prob = 0.5)))

plot(table(Y))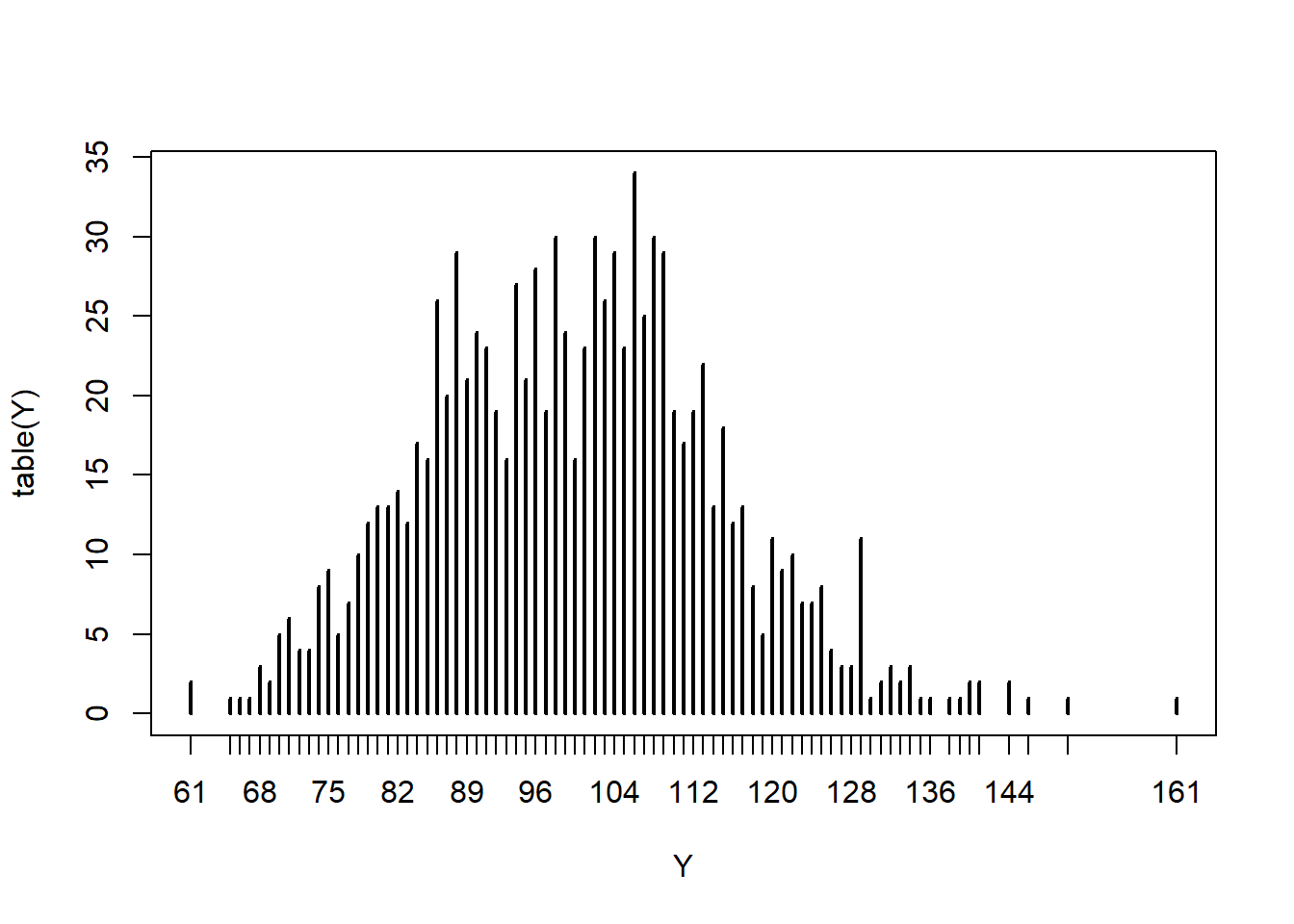

\(X\)が幾何分布でも、足し合わせた変数\(Y\)の分布は正規分布っぽくなった⁴。

というわけで、サンプルサイズが多い→正規分布で近似できるというのは間違い（あるいは語弊がある）。ちゃんと確率変数の特徴に見合った確率分布を選びたいですね。