6/16/24 the content of this post is officially out in Population Ecology.
I never thought I would do this in my life; this is certainly not something I want to do. Yet, there is no option but to write this post because otherwise, the recent paper by Carraro and Altermatt (2022) invalidates past research and future work on scale invariance for unfair reasons. I posted full mathematical details as a preprint here (including the re-analysis of their data). I want to make clear that I do agree (100%!) with their opinion that Optimal Channel Networks (OCNs) have very high potential to advance the ecological understanding of stream communities. My point below is not to disregard the usefulness of OCNs by no means.
As a stream ecologist, I’m interested in how a stream network structure dictates ecological dynamics - so the assessment of stream network structure is a critical component in my research. I use “branching probability” to measure network complexity, i.e., the probability of observing a single joining tributary per unit river distance. In my past studies (Terui et al. 2018, 2021), I referred to branching probability as a variable reflecting the “scale invariance” of fractal rivers. In contrast, Carraro and Altermatt 2022 concluded in their paper, “…we show that an alleged property of such random networks (branching probability1) is a scale-dependent quantity that does not reflect any recognized metric of rivers’ fractal character…” I was shocked because if this is true, what I had been saying in my papers was very wrong. However, after careful reading, this conclusion turned out to be due to the author’s misuse of the term “scale invariance.” The conclusion derived from their analysis must have been the complete opposite, “branching probability is a scale-invariant feature that reflects the fractal nature of rivers,” as explained below.
Premise
Scale-invariance refers to a phenomenon in which a self-similar structure appears (almost) infinitely as you increase the resolution of the measurement. The most famous example of scale invariance is the length of the UK coastline. Mandelbrot 1967 used a ruler length \(x\) as a scale of observation (= the resolution of the measurement; see red-line segments in the image below) to measure the length of coastline \(y\) and expressed it as a function of scale \(x\), \(y = f(x)\).
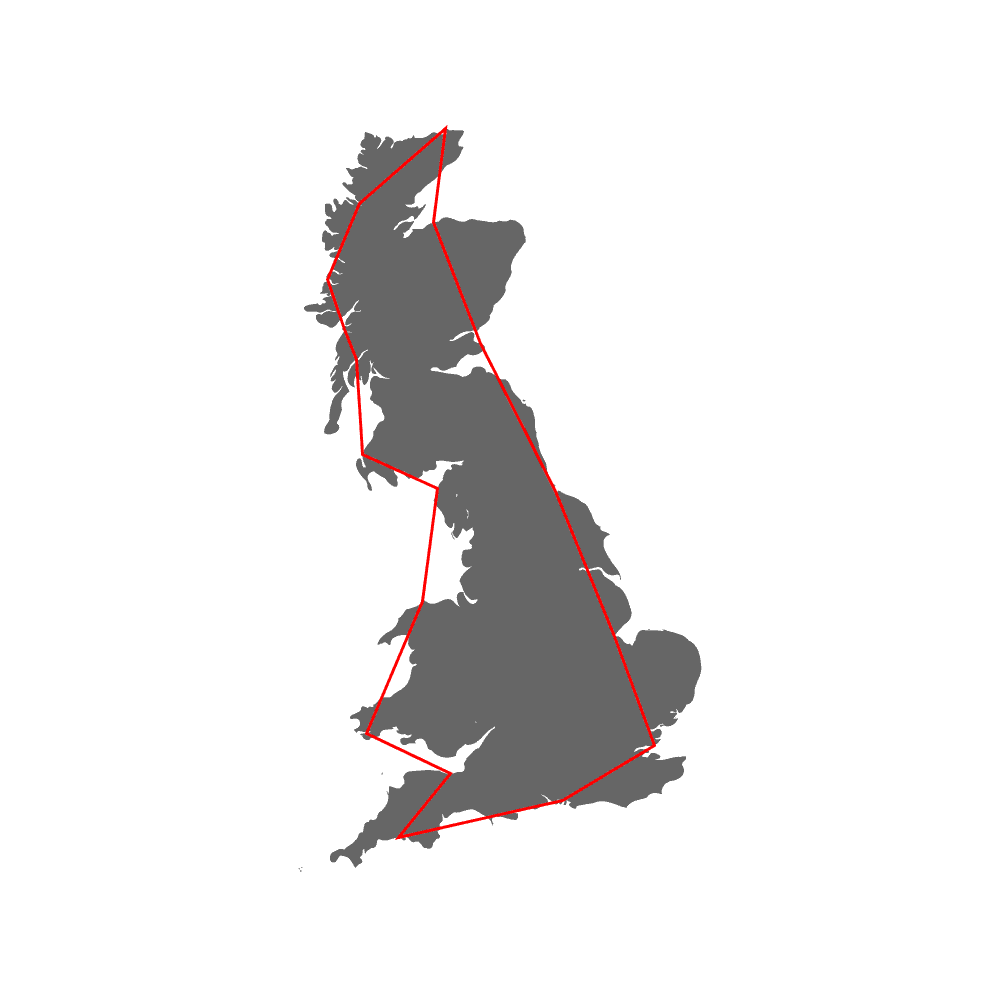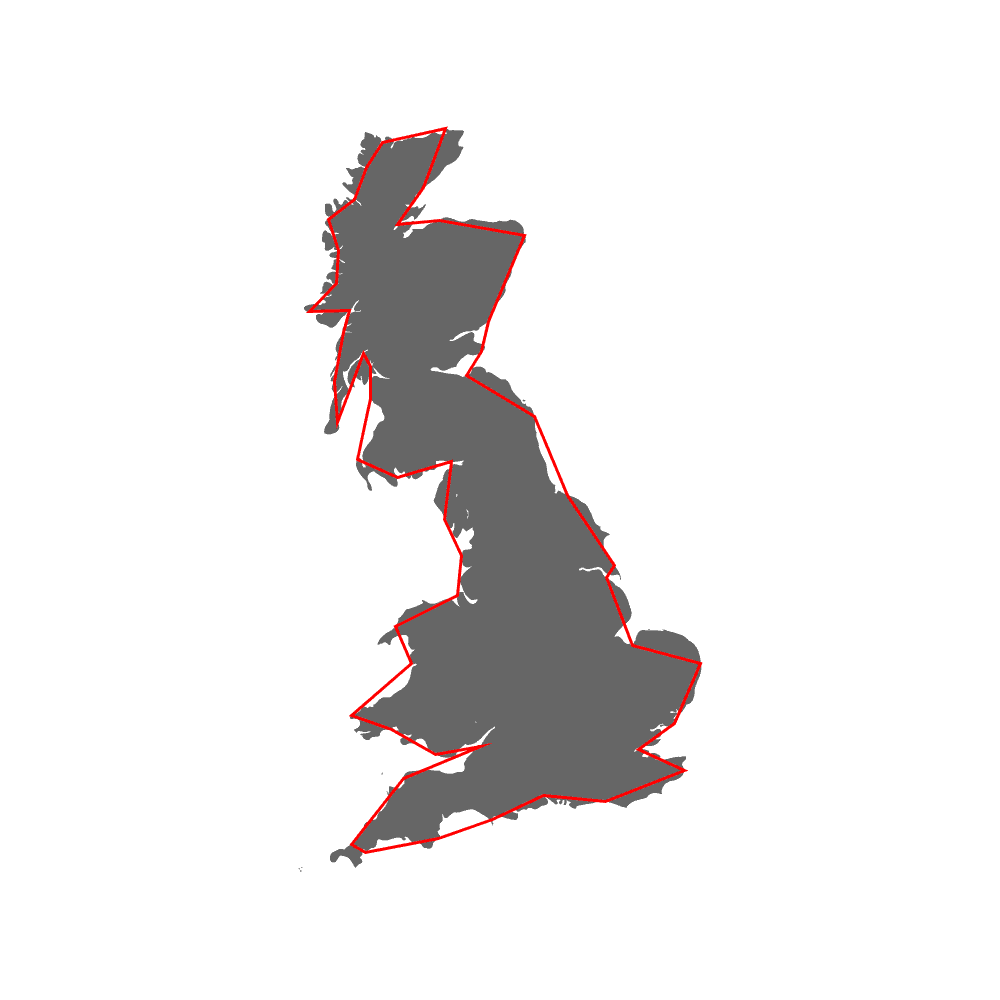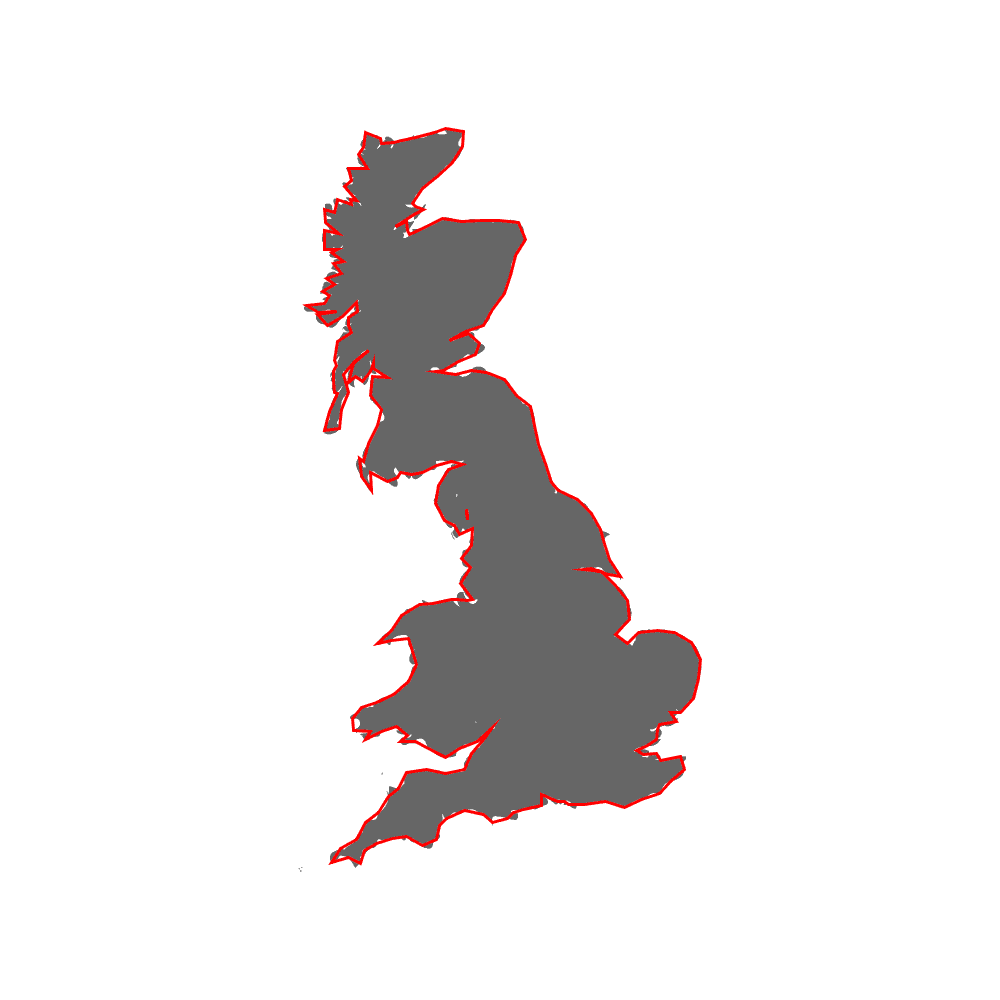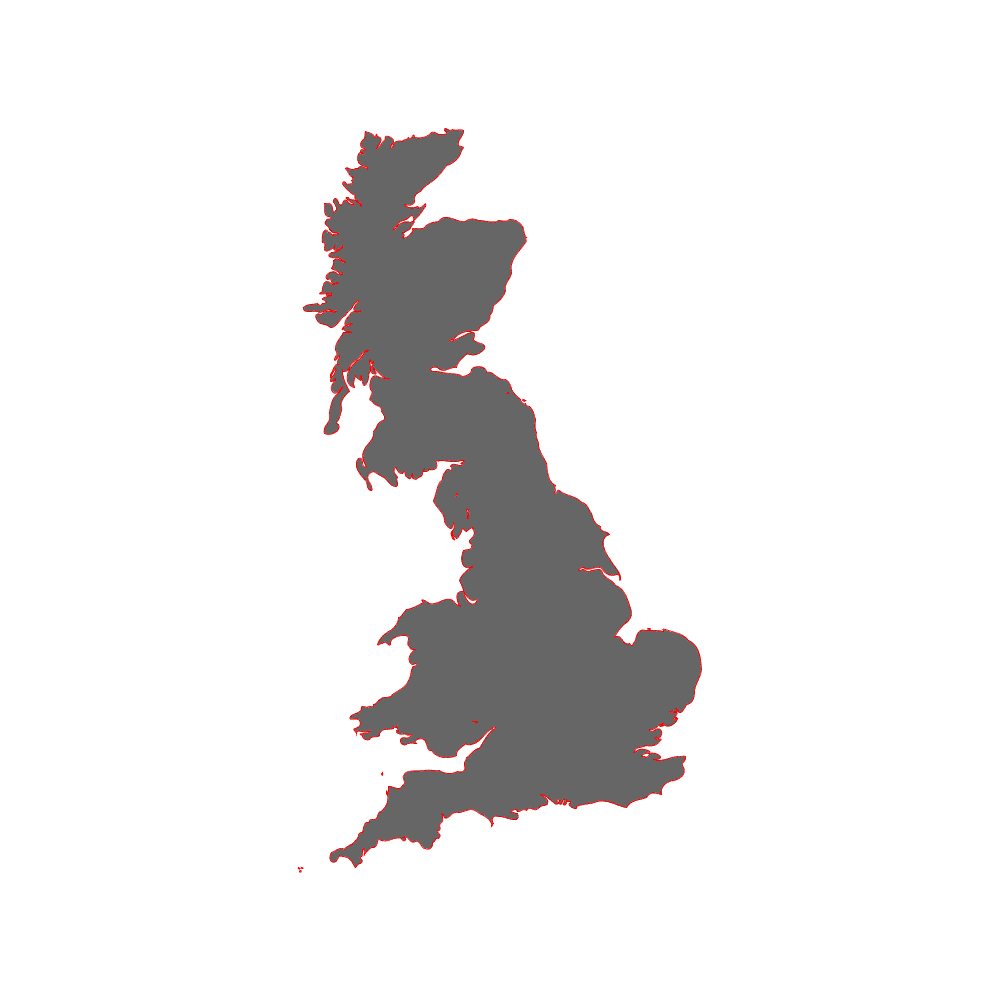
When Mandelbrot measured the total length of the coastline as multiples of the ruler length \(x\) (i.e., \(N(x)x\), where \(N(x)\) is the number of rulers needed given the length \(x\)), the length (function \(f(x)\)) diverged to reach infinity as \(x \rightarrow 0\), because he found finer, but similar zig-zag patterns over and over as he uses a shorter ruler (see the figure below; this is just for a graphical example). This observation is realized as a power-law scaling of length \(y\):
\[ y = f(x) = cx^{-z} \]
where \(c\) is the scaling constant and \(z\) the scaling exponent. In this equation, the observed variable \(y\) reaches infinity as \(x \rightarrow 0\), reflecting the fractal nature of the coastline. In contrast, scale dependent objects do not show this “scaling.” For example, if we consider a perfect square (\(500\) km on a side), the perimeter (\(500 \times 4 = 2000\) km) remains constant regardless ruler length \(x\). This is a property called “non-scaling” (see the gray lines in the figure below).

In a power law, the shrinkage/extension of scale \(x\) will result in a simple multiplication of the observation \(y\). For example:
\[ y'=f(2x)=c(2x)^{-z} = 2^{-z}cx^{-z} = 2^{-z}f(x) = 2^{-z}y \]
Since \(y'\) is a simple multiplication of the original object \(y\) (\(y\) is the part of \(y'\)), this proves that the structural property is retained across observation scale \(x\). Therefore, the observed object \(y\) expressed as a function of scale \(x\) (\(y\) equals \(f(x)\)) is said to be scale invariant when it follows a power-law2. Often confused, but “scaling” and “the lack of characteristic scale” are the properties associated with scale-invariance3.
| Object type | Property | Example used in Madelbrot 1967 |
|---|---|---|
| Scale invariant | scaling, the lack of characteristic scale | the length of a coast line |
| Scale dependence | non-scaling, the existence of characteristic scale | the perimeter of a perfect circle |
What Carraro & Altermatt found
Carraro & Altermatt 2022 reported that the branching probability follows a power law of observation scale \(A_T\) using virtual networks called Optimal Channel Networks (Equation (1) in the original article). In addition, they also observed the power-law scaling of branching probability in real rivers (see the log-log plot in Figure 3 in the original article).
Nevertheless, they concluded “an alleged property of such random networks (branching probability) is a scale-dependent quantity that does not reflect any recognized metric of rivers’ fractal character…” This is the complete opposite as it has been defined in the literature of scale invariance (and “alleged”…!!? This word killed me…). Instead, the correct conclusion derived from their results must have been “branching probability is a scale-invariant feature that reflects the fractal nature of rivers.”4 They also used other key terms in a completely opposite way – for example, the term “scaling” is used as if it describes a property of a scale-dependent object. Shockingly (at least for me), they seriously criticized past research by expanding their arguments based on this misuse of the term throughout their manuscript (see here for full details).
If the misuse of these key terms is approved, it invalidates – regardless of the author’s intention – the entire body of literature in scale invariance since the 1960s because their claim is essentially what we have been calling “scale-invariant” is “scale-dependent.” Is this…acceptable?
Practical problem
The fundamental problem in Carraro & Altermatt (the misunderstanding of what we call scale invariant…) is actually very common for those who just started learning this concept – honestly speaking, I fell into the same pitfall when I started studying scale invariance. As such, I am very worried about the potential educational consequences of this paper – many of the potential readers (ecologists) will get tricked VERY EASILY. This misuse is as deep as swapping the terms “competition” and “mutualism,” if ecological analogy allowed. The term scale invariance is mathematically and uniquely defined, and there is no room for arguments in its definition.
The authors coined the term “branching ratio” (the inverse of mean link length) by claiming that branching probability is not a probability – this is simply a misunderstanding. Branching probability has been defined as a cumulative distribution function of link length. Branching ratio is the rate parameter characterizing the link length distribution.↩︎
Formally, a function \(f(x)\) is said to be scale invariant if it suffices the following equation: \(f(\lambda x) = \lambda^z f(x)\), where \(\lambda\) is an arbitrary constant and \(z\) is the scaling exponent. A power law is one example of satisfying this equation.↩︎
These terms are clearly explained in the textbook by Rodriquez-Iturbe & Rinaldo 2001:
↩︎Self-similarity is a concept associated with fractal geometry that refers to invariance…The smaller structures are identical to the large-scale ones when they undergo an expansion in their scale. This similarity of parts to the whole is called self-similarity, and it is described by the lack of any characteristic scale, a property called scaling. (p.99, Rodriquez-Iturbe & Rinaldo 2001)
Well, branching probability is proven to be scale invariant in Peckham and Gupta 1999 to begin with…↩︎