Rでシミュレーション3 - foreach

パラメータセットを用意する

以前作った個体群動態のシミュレーションモデルを、ここの例題として再度利用する：

\[ ln~n_{t+1} = ln~\lambda + ln~n_t + \epsilon_t\\ \epsilon_t \sim N(0,\sigma_{\epsilon}^2) \]

前年の個体数\(n_{t}\)に集団増加率\(\lambda\)が掛け算され、翌年の個体数\(n_{t+1}\)が決まるが、そこにはランダムな環境変動の影響（\(\epsilon_t\)）もある、というものであった（上の式では対数スケールのため足し算になっている）。これをコードとして書き下し、関数化したものが以下：

sim_geomodel <- function(n_step,
                         lambda,
                         sd_eps,
                         n1 = 10) {
  
  log_n <- NULL
  log_n[1] <- log(n1)
  eps <- rnorm(n = n_step, mean = 0, sd = sd_eps)
  
  for(t in 1:(n_step - 1)) {
    log_n[t + 1] <- log(lambda) + log_n[t] + eps[t]
  }
  
  n <- exp(log_n)
  
  df_dynamics <- dplyr::tibble(n_step = 1:n_step,
                               n = n)
  
  return(df_dynamics)
}

この関数sim_geomodelを使い、パラメータの値を変えた時に、50年後の個体数の予測値がどう変わるのか調べてみよう。パラメータを変えながらパターンを予測することで、どのパラメータが集団動態にどんな影響を及ぼすのかを調べることができる。今回の場合、パラメータは二つあるので（lambda, sd_eps）、これらのパラメータセットを作るところから始める。パラメータセットを作るには、パラメータ値のすべての組み合わせを考える必要がある。この場合、expand.grid()という関数が役立つ：

lambda <- c(1.1, 1.3)
sd_eps <- c(0.1, 0.5)

param_set <- expand.grid(lambda = lambda,
                         sd_eps = sd_eps)

print(param_set)

##   lambda sd_eps
## 1    1.1    0.1
## 2    1.3    0.1
## 3    1.1    0.5
## 4    1.3    0.5

この関数を使うと、すべてのパラメータ値の組み合わせを考えたデータフレームを生成してくれるので、非常に便利。このパラメータセットの組み合わせを一つのシナリオとして、それぞれのシナリオの下で集団動態を100回シミュレートする。

foreachの導入

それぞれのシナリオの下で50年後の個体数の予測をしてみることにするが、このときforeachを導入する。というのも、今回のケースは問題にならないが、今後並列化などを視野にいれたとき、この関数に慣れておいたほうがいいためである（foreachの使い方はこちらを参照）。全体としてはこんな形で書き下すことができる。

pacman::p_load(foreach,
               tidyverse)

n_rep <- 100

result <- foreach(k = 1:nrow(param_set),
                  .combine = dplyr::bind_rows) %do% {
          
          df_rep <- foreach(i = 1:n_rep,
                            .combine = dplyr::bind_rows) %do% {
                              
                              df_dyn <- sim_geomodel(n_step = 50,
                                                     lambda = param_set$lambda[k],
                                                     sd_eps = param_set$sd_eps[k],
                                                     n1 = 10)
                                
                              y <- dplyr::filter(df_dyn, n_step == 50)
                              re <- dplyr::tibble(n_rep = i,
                                                  param_set[k,],
                                                  n50 = y$n)
                              
                              return(re)
                            } 
          
          return(df_rep)
        }

print(result)

## # A tibble: 400 × 4
##    n_rep lambda sd_eps   n50
##    <int>  <dbl>  <dbl> <dbl>
##  1     1    1.1    0.1  384.
##  2     2    1.1    0.1 1537.
##  3     3    1.1    0.1 1334.
##  4     4    1.1    0.1 2973.
##  5     5    1.1    0.1  576.
##  6     6    1.1    0.1  518.
##  7     7    1.1    0.1 1086.
##  8     8    1.1    0.1  130.
##  9     9    1.1    0.1 1768.
## 10    10    1.1    0.1  329.
## # … with 390 more rows

以下、個別の要素について。まずはdf_repでなにをやっているか。

df_rep <- foreach(i = 1:n_rep,
                  .combine = "bind_rows") %do% {
                    
                    df_dyn <- sim_geomodel(n_step = 50,
                                           lambda = param_set$lambda[k],
                                           sd_eps = param_set$sd_eps[k],
                                           n1 = 10)
                      
                    y <- dplyr::filter(df_dyn, n_step == 50)
                    re <- tibble(n_rep = i,
                                 param_set[k,],
                                 n50 = y)
                    
                    return(re)
                  } 

この部分が一つのシミュレーションの反復計算になっている。df_dynに計算結果が格納され、その結果の内からn_step == 50となるシミュレーション結果を抽出している（dplyr::filter(df_dyn, n_step == 50)）。次に、この結果をデータフレームtibbleとして保存している（反復回数i、計算に使われたパラメータセットの値param_set[k,]、そのパラメータセットのもとでの計算結果y$n）。こうして結果を保存することで、「どのパラメータセットのもとでどんな予測がなされたのか」を簡単に図示できる。このforeachのくくりの中ではパラメータセットは固定されているので、同じパラメータセットのもとでの反復間のばらつきをみることができる。

さらに、このセットをさらにforeachでくくり、パラメータセットを変えるように指定することで、各パラメータセットのもとで指定された数の反復がなされるようになっている。

result <- foreach(k = 1:nrow(param_set),
                  .combine = "bind_rows",
                  .packages = "dplyr") %do% {
          
          df_rep <- #foreach contents
          
          return(df_rep)
        }

Plotを描く

この結果をもとに、それぞれのパラメータセットのもとで、50年後の個体数の予測値がそれぞれどうなっているか図示する。resultはTidyフォーマットになっているので、ggplotとの相性がよい。

result <- result %>% 
  mutate(sd_eps_label = recode(sd_eps,
                              `0.1`= sprintf('"Low SD"~(sigma[epsilon]=="%.2f")', sd_eps),
                              `0.5`= sprintf('"High SD"~(sigma[epsilon]=="%.2f")', sd_eps)
                     )
         )

result %>% 
  ggplot(aes(y = n50, x = factor(lambda))) +
  geom_boxplot(alpha = 0.5, outlier.shape = NA) +
  geom_jitter(alpha = 0.5, size = 0.5) +
  facet_wrap(facets = ~sd_eps_label, 
             ncol = 2,
             labeller = label_parsed) +
  scale_y_continuous(trans = "log10") +
  xlab(expression("Population growth rate"~lambda)) +
  ylab("Population size in year 50") +
  theme_bw()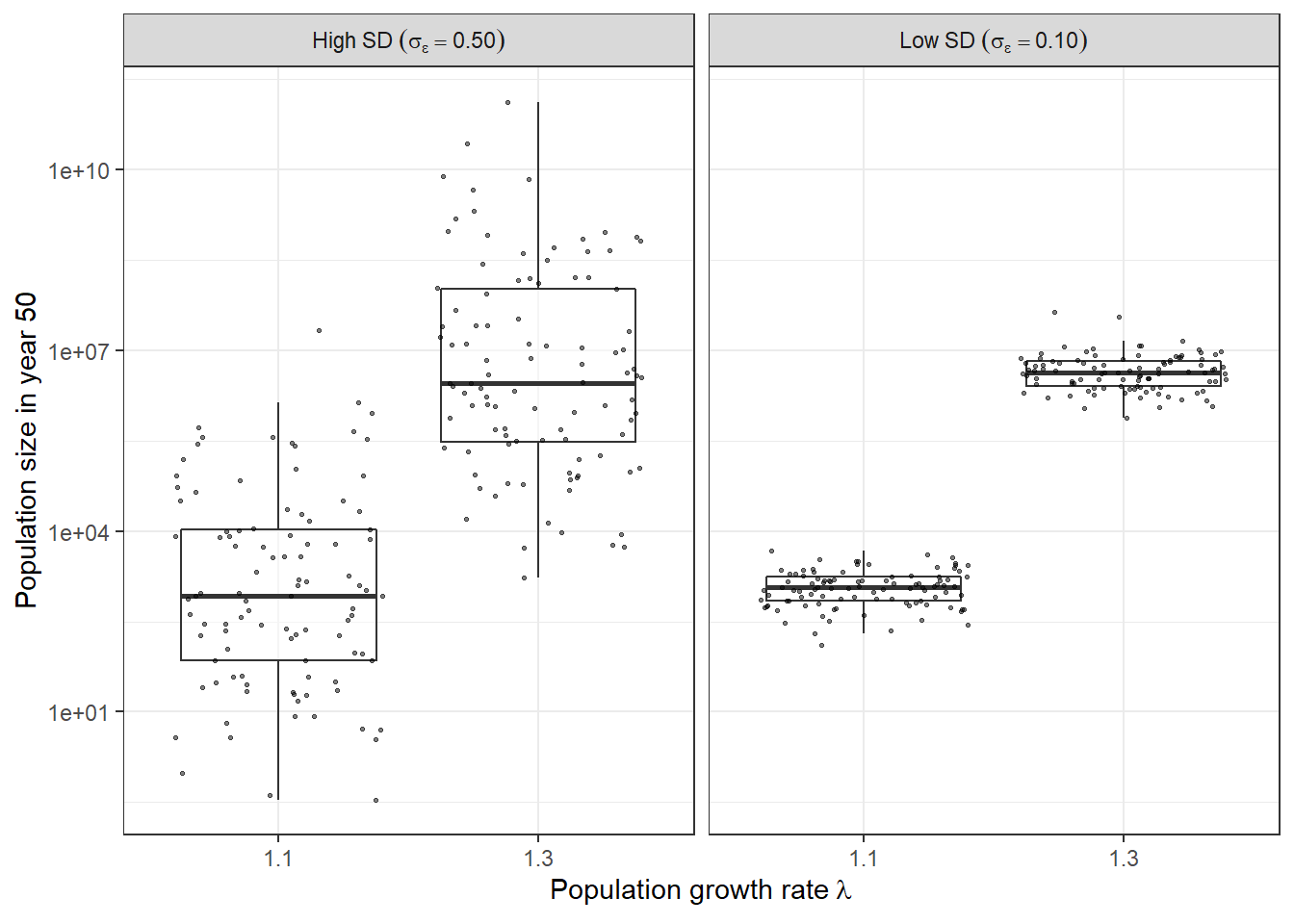

当然だけど、個体群増加率\(\lambda\)が大きいほど集団はより大きく成長し、環境変動\(\sigma_{\epsilon}\)が大きいほど50年後の個体数のばらつき大きいことがわかる。