Rでシミュレーション2 - function

functionの導入

function関数を使うことで一度書いたモデルを使いまわすことができる。最初からシミュレーションモデルを関数化すると説明が煩雑になってしまうので、まずは変動係数CVを推定する関数mycv なるものを作ってみよう。まずは正規分布に従う乱数をrnormを使って生成する。

# 100 random values following a normal distribution
set.seed(123) # for reproducibility
y <- rnorm(n = 100, mean = 50, sd = 25)

# show the first 10 elements
print(y[1:10])

##  [1] 35.98811 44.24556 88.96771 51.76271 53.23219 92.87662 61.52291 18.37347
##  [9] 32.82868 38.85845

変動係数は以下のスクリプトで推定できる。

cv <- sd(y) / mean(y)
print(cv)

## [1] 0.4366692

しかし、なんだか毎回二つの関数sd とmean を組み合わせて変動係数を計算するのは面倒くさい。なので、これらの作業を一挙にやってくれる関数をつくってみよう。

mycv <- function(x) {
  cv <- sd(x) / mean(x)
  return(cv)
}

x という引数に基づいて、SDを平均で割るという作業を自動的にやってくれる関数mycv を定義している。function() のカッコの中に引数として使いたい変数をいれておく。そうすると、そこに使ってほしい値をぶち込むと、関数内で定義された作業を自動的に行ってくれる。return のところでは、何を計算結果（返り値）として返してほしいかを指定している。早速mycv を使ってみる。以下では、x = y とし、関数内のx にy を「代入」している。

mycv(x = y)

## [1] 0.4366692

この関数はとてもシンプルな計算をまとめているが、もっと複雑な内容を関数化することも可能だ。例えば、CVだけでなく、平均とSDも返す関数にしたいならば：

mycv <- function(x) {
  
  mu <- mean(x)
  sigma <- sd(x)
  cv <- sd(x) / mean(x)
  
  return(list(mu = mu,
              sigma = sigma,
              cv = cv)
         )
}

複数の返り値を持たせてやるときに気を付けなければならないのは、return() の中身をリスト化しなければならないことだ。そうしないと、関数自体は定義できても、その関数を使う際にエラーがでてしまう。複数の返り値がある場合、それぞれの要素に$でアクセスできる。

estimate <- mycv(x = y)

estimate

## $mu
## [1] 52.26015
## 
## $sigma
## [1] 22.8204
## 
## $cv
## [1] 0.4366692

estimate$cv

## [1] 0.4366692

estimate$mu

## [1] 52.26015

estimate$sigma

## [1] 22.8204

関数化することはできたが、この簡単な関数にも実は落とし穴がある。次のデータをこの関数にいれてみよう。

z <- rnorm(100, mean = 50, sd = 25)
z[sample(1:100, size = 10)] <- NA 

上のデータでは、先ほどと同じように100個の正規分布に従う乱数を使っているが、そのうちの10個がNAに置き換えられている。このデータをmycvに渡すと返り値がすべてNAになってしまう。

mycv(x = z)

## $mu
## [1] NA
## 
## $sigma
## [1] NA
## 
## $cv
## [1] NA

これはもともとmean()とsd()がNA入りのデータに対応していないからである（na.rm = TRUEとすれば取り除いてくれるが）。NAがある場合には、事前にNAを入力データから消去する処理を加えた関数にしてみよう。

mycv <- function(x) {
  
  # remove NAs if any
  if(any(is.na(x))) {
    x <- na.omit(x)
    message("NA detected in the data; removed before the estimation")
  }
  
  mu <- mean(x)
  sigma <- sd(x)
  cv <- sd(x) / mean(x)
  
  return(list(mu = mu,
              sigma = sigma,
              cv = cv)
         )
}

if()は、カッコ内の条件式がTRUEである場合にのみ、{}内の作業を実行するよう指定する関数である。この場合、any(is.na(x))とすることで、xに一つでもNAがある場合にはそれを取り除く作業を行うよう指定している。この際に、NAが取り除かれたことを明示的に解析者に示すために、message("NA detected in the data; removed before the estimation")というメッセージを表示するように指定している。もう一度zを代入してみる。

# z contains NAs in the data
mycv(x = z)

## NA detected in the data; removed before the estimation

## $mu
## [1] 46.06076
## 
## $sigma
## [1] 23.8327
## 
## $cv
## [1] 0.5174186

NAが取り除かれたことを示すメッセージとともに、残されたデータから推定された平均、SD、CVが返されている。データにNAがない場合、このメッセージは表示されない。

# y does not contain NAs in the data
mycv(x = y)

## $mu
## [1] 52.26015
## 
## $sigma
## [1] 22.8204
## 
## $cv
## [1] 0.4366692

シミュレーションを関数化

ではfuncionを使って、前回つくったシミュレーションモデルを関数化してみる。

sim_geomodel <- function(n_step,
                         lambda,
                         sd_eps,
                         n1 = 10) {
  
  log_n <- NULL
  log_n[1] <- log(n1)
  eps <- rnorm(n = n_step, mean = 0, sd = sd_eps)
  
  for(t in 1:(n_step - 1)) {
    log_n[t + 1] <- log(lambda) + log_n[t] + eps[t]
  }
  
  n <- exp(log_n)
  
  df_dynamics <- dplyr::tibble(n_step = 1:n_step,
                               n = n)
  
  return(df_dynamics)
}

モデルスクリプトをfunction内に移しただけだが、大きく異なる点がある。n1、lambda、n_step、およびsd_epsを関数の引数（使用者が任意のインプットを指定できる）として定義することで、様々なシナリオのもとでシミュレートしやすくなっている。ここではn1 = 10としているが、「この引数はデフォルトで10という値を与える」という意味になる（この関数の使用者が何も値を指定しなければ、勝手にn1 = 10として計算を進める）。それ以外の引数は、明示的に値を与えなければならない。また、アウトプットはTime stepと個体数を対応させたtibble形式にしてある。こうすることで後の図示がずっと楽になる。早速この関数を使ってみる。

re <- sim_geomodel(n_step = 20,
                   lambda = 1.1,
                   sd_eps = 0.1)

print(re)

## # A tibble: 20 × 2
##    n_step     n
##     <int> <dbl>
##  1      1  10  
##  2      2  11.0
##  3      3  11.1
##  4      4  11.6
##  5      5  10.6
##  6      6  12.1
##  7      7  12.7
##  8      8  14.4
##  9      9  15.4
## 10     10  18.9
## 11     11  21.1
## 12     12  30.5
## 13     13  34.5
## 14     14  37.8
## 15     15  37.7
## 16     16  42.3
## 17     17  42.2
## 18     18  49.1
## 19     19  48.6
## 20     20  55.9

plot(n ~ n_step,
     data = re,
     xlab = "Time step",
     ylab = "Number of individuals",
     type = "o")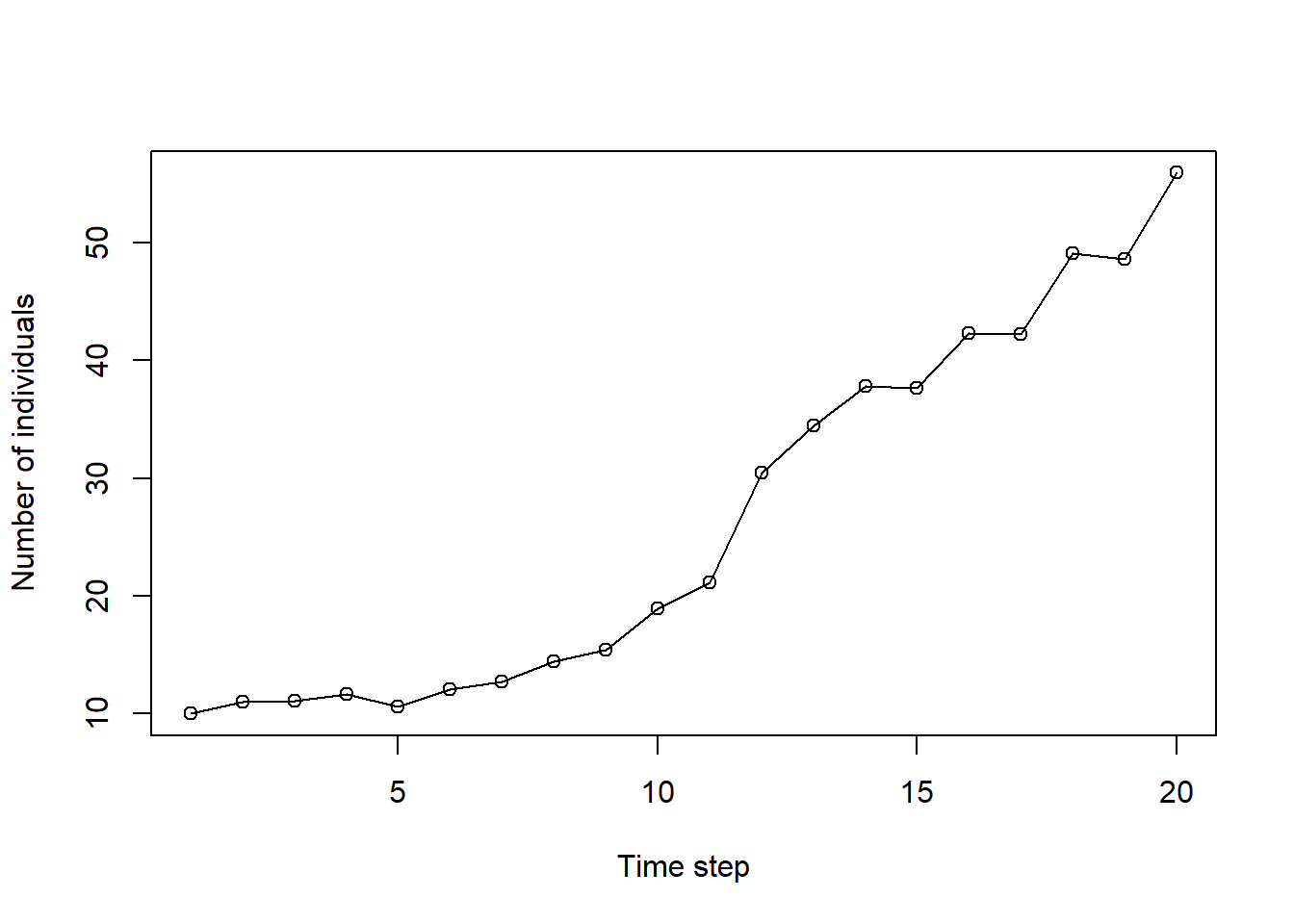

このモデルでは、年によって集団増加率がランダムに変動するような仮定がおいてある（計算のたびに個体数の変化の仕方は変わる）。そのため、同じ作業を繰り返し、結果がどれくらいばらつくのかを見みたい。この作業が関数化されているとぐっと楽になる。for構文を使ってやってみよう。せっかくなので、アウトプットはtidyverseで扱いやすいようtidy形式にする。

library(tidyverse)

# create output dataframe
df_dynamics <- tibble()

# define n_step
n_step <- 50

for(i in 1:5) {
  
  df_subset <- sim_geomodel(n_step = n_step,
                            lambda = 1.1,
                            sd_eps = 0.1)
  
  # add replicate number column
  df_subset <- df_subset %>% 
    mutate(n_rep = i)
  
  # combine replication subsets
  df_dynamics <- bind_rows(df_dynamics, df_subset)
  
}

print(df_dynamics)

## # A tibble: 250 × 3
##    n_step     n n_rep
##     <int> <dbl> <int>
##  1      1 10        1
##  2      2  9.40     1
##  3      3 11.7      1
##  4      4 13.7      1
##  5      5 13.5      1
##  6      6 14.6      1
##  7      7 14.6      1
##  8      8 15.1      1
##  9      9 17.4      1
## 10     10 20.9      1
## # … with 240 more rows

50ステップのシミュレーションを5回繰り返したので、それをレプリケーションごとに図示してみる。

g <- ggplot(df_dynamics) +
  geom_line(aes(x = n_step, y = n, color = factor(n_rep))) +
  geom_point(aes(x = n_step, y = n, color = factor(n_rep)), alpha = 0.2) +
  ylab("Number of individuals") +
  xlab("Time step")
  
print(g)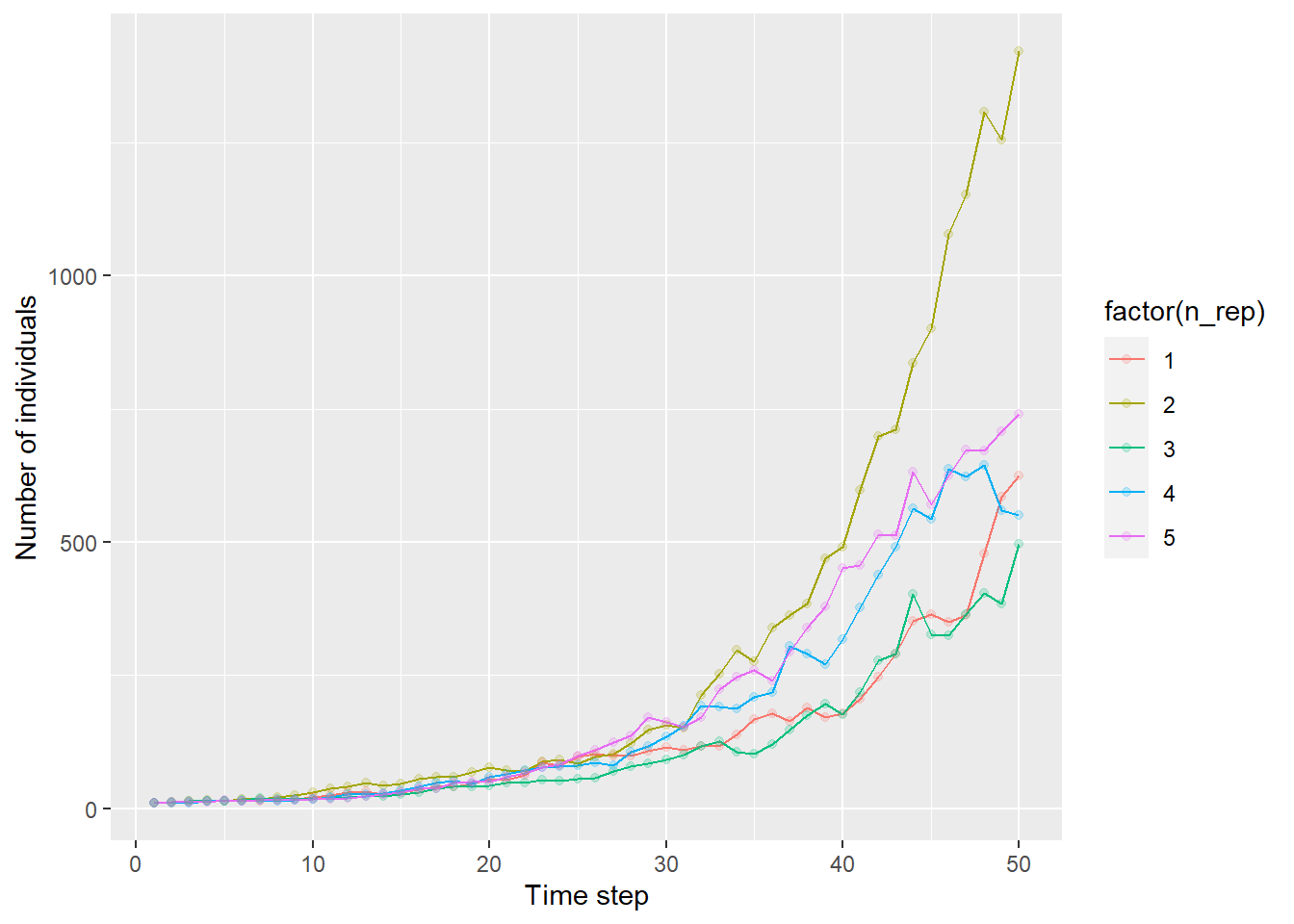

集団の増加の仕方は、繰り返すごとに大きく異なることが見て取れる。これらの値の平均と標準誤差を計算する。対数をとってから平均をとることで、幾何平均とそのばらつきをみることにしよう。

# summarize df_dynamics
df_summary <- df_dynamics %>% 
  group_by(n_step) %>% 
  summarize(log_mean_n = mean(log(n)), # mean of log-transformed n
            log_sd_n = sd(log(n))) %>%  # sd of log-transformed n
  mutate(log_upper = log_mean_n + log_sd_n,
         log_lower = log_mean_n - log_sd_n) %>% 
  mutate(mean_n = exp(log_mean_n),
         upper = exp(log_upper),
         lower = exp(log_lower))
  
print(df_summary)

## # A tibble: 50 × 8
##    n_step log_mean_n log_sd_n log_upper log_lower mean_n upper lower
##     <int>      <dbl>    <dbl>     <dbl>     <dbl>  <dbl> <dbl> <dbl>
##  1      1       2.30   0           2.30      2.30   10    10   10   
##  2      2       2.38   0.125       2.50      2.25   10.8  12.2  9.50
##  3      3       2.52   0.120       2.64      2.40   12.4  14.0 11.0 
##  4      4       2.60   0.0885      2.69      2.51   13.4  14.7 12.3 
##  5      5       2.63   0.0597      2.69      2.57   13.8  14.7 13.0 
##  6      6       2.72   0.108       2.83      2.61   15.1  16.9 13.6 
##  7      7       2.78   0.118       2.90      2.67   16.2  18.2 14.4 
##  8      8       2.81   0.137       2.95      2.68   16.7  19.1 14.5 
##  9      9       2.89   0.182       3.07      2.71   18.0  21.5 15.0 
## 10     10       3.02   0.231       3.25      2.79   20.4  25.7 16.2 
## # … with 40 more rows

繰り返し間の幾何平均とそのばらつきを合わせて図示する。

ggplot(df_summary) +
  geom_line(aes(x = n_step, y = mean_n)) + # line for mean n
  geom_ribbon(aes(x= n_step, ymin = lower, ymax = upper),
              alpha = 0.2) # sd around the mean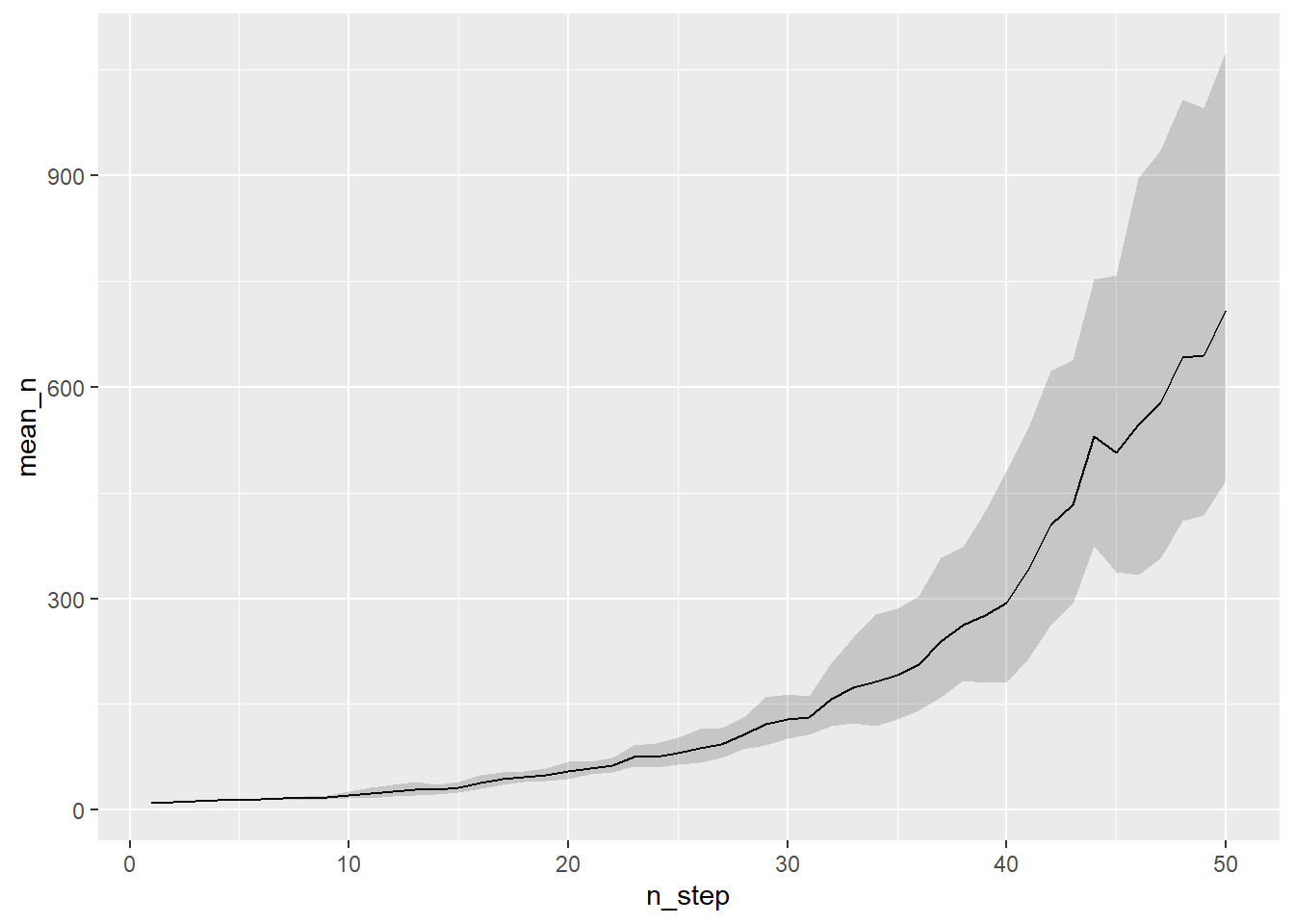

実際のシミュレーションでは100-1000回ほど繰り返し、その平均や中央値を「あるシナリオのもとで期待されるパターン」として解釈する。 今回の場合、個体群増加率lambda = 1.1、初期個体数n1 = 10、そして環境変動の大きさsd_eps = 0.1の組み合わせが「シナリオ」に対応する。これらの値を変えたら集団増加のパターンはどうなるだろうか？そのためにはこれらの値を変えながら、パターンの変化をみることになる。例えばlambdaについては1.1と1.5を、sd_epsは0.1と1.0を考えるとしよう（n1はその効果に興味がないので10に固定したとする）。そうすると、この二変数の組み合わせは2 x 2で4通り、それぞれシミュレーションを1000回繰り返すとしたら1000 x 4で4000回シミュレーションを回すことになる。このあたりの作業を自動化しないとやっていられないので、次はその方法を書こうと思う。