なぜシミュレーション？

生態学に慣れ始めてきたころ、いわゆる「理論研究」と言われる類の論文も読み始めるようになった。最初は難解で何をしているのかわからなかったが、分かってくるととても力強いアプローチだなぁと感じるようになり、自分で作ってみたいと思うようになった。というのも、私はフィールドを中心に研究をしていたけれども、野外のデータはあまりにも雑多で、その解釈に困ることが多かったからだ。例えば、ある魚と別の魚が餌をめぐる競争関係に興味があり、「この二種は競争関係にあるので、一方の個体数が多い場所では、もう一方の個体数は少なくなる」という仮説を立てたとしよう。野外で両種の個体数の間に負の相関が認められたとしても、「おお仮説通りのパターンだ、競争に違いない！」と単純に喜ぶことはできない。同じパターンを生み出す仕組みがあまりにもたくさんあるからだ（両者の好きな環境が全く異なるだけかもしれない）。

こうした理由から、自分がフィールドで集めたデータをもとに論文を書くとき、（特にDiscussionで）もどかしい思いをする。思いっきり「これだ！」と断言したいのに、あれやこれやと言い訳しなければならないからだ。実験で検証可能な仮説ならば、実験するに越したことはない。しかし、見たい現象が生態系スケールとかになってくると、実験などほぼ不可能だ。できたとしても億単位の研究費が必要になる。

そんなとき、シミュレーションが役に立つ。ある仕組みをこちらで勝手に想定し、そこから導かれるパターンがどんなものかを見るのがシミュレーションだ（生態学の数理モデルが全般的にそうですが）。つまり、観察されたパターンから仕組みを推論する統計モデリングの全く逆のことをするといってもいい（Figure 1）。興味のある仕組み以外を排除あるいはコントロールできるので、その仕組みがどんな時にどんなパターンを生み出すのか知ることができる。

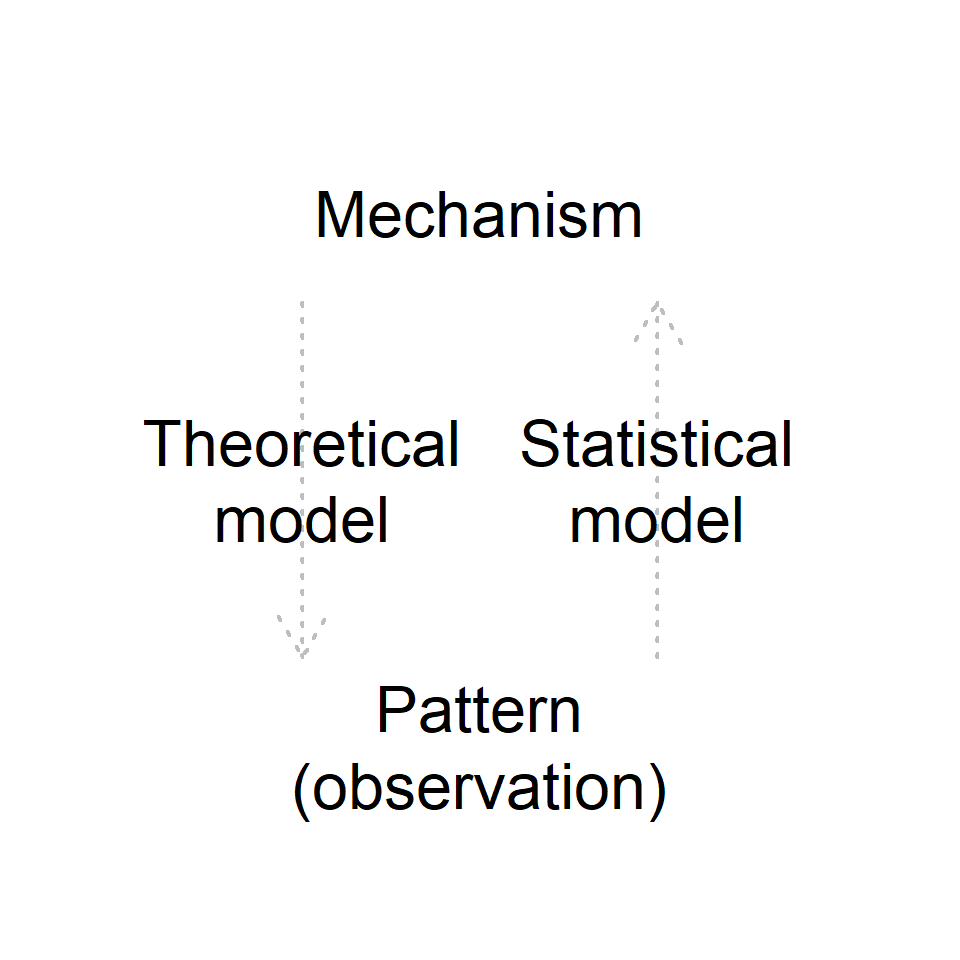
Conceptual diagram for the roles of theoretical and statistical models. Theoretical models (generally) predict patterns under certain mechanisms (and assumptions) while statistical models infer mechanisms behind observed patterns

Figure 1: Conceptual diagram for the roles of theoretical and statistical models. Theoretical models (generally) predict patterns under certain mechanisms (and assumptions) while statistical models infer mechanisms behind observed patterns

と、ここまでは論文を読んでいれば納得できるのだが、いかんせんどうやってスクリプトを書けばいいのかわからない…というのが学生のころの悩みだった。統計解析のリソースはオンラインにかなり落ちているので自分でいくらでも勉強できたが、シミュレーションモデルは本当にスクリプトのリソースが少ない。あったとしても、これからやろうとしている人向けには書かれていない。それが今回の（たぶんシリーズ的に）書こうと思っているポストのモチベーション。

for loop

こまごましたことはあるのだが、まずはfor構文をつかって簡単なシミュレーションモデルを作ってしまおう。for構文とはなんぞや、という人もいるかもしれないので、ここで簡単に説明しておく。端的にいうと、コンピュータに「同じ作業を繰り返せ」と指令するコマンド。for(i in 1:3) { XXX }という形で書くのだが、これはiがイテレータと呼ばれるもので、繰り返しのユニットに対応するものだ。このスクリプトで言えば、「XXXという作業を1から3まで回してほしい」と指令している。これだとわかりにくいので、下の例をみてみよう。

# create a vector with 11, 12, 13
y <- NULL
x <- 11:13

for(i in 1:3) {
  y[i] <- x[i] * 2
}

ここではyとxというオブジェクトを作り、xのほうに11から13の値を代入している。やりたいことは、xの値をそれぞれ2倍することである。for構文の中身は次のように展開できる（下付き文字がイテレータに対応している）。

\[ y_1 = 2x_1\\ y_2 = 2x_2\\ y_3 = 2x_3\\ \] yの中身を見てみると、それぞれ二倍されていることがわかる。

y
## [1] 22 24 26

ぶっちゃけこれだけならばy <- 2 * xで同じことができてしまうのでfor構文を使う必要など全くないのだが、もっと複雑な作業を繰り返しさせたいときにはfor構文に頼る必要がある。

集団動態モデル

このfor構文を使って、早速「シミュレーションモデル」を作ってみよう。ここでは集団サイズnが集団増加率lambdaにしたがって増えることを想定し、以下のようなモデルを考える。

\[ n_{t+1} = \lambda n_{t} \]

時間\(t+1\)における集団サイズ\(n_{t+1}\)は、その一つ手前（1年前とか）の集団サイズ\(n_t\)に\(\lambda\)を掛け算したものになっている、とするモデル。これは先のfor構文を使うと次のように書くことができる。

n <- NULL
n[1] <- 10 # initial population size
lambda <- 1.1

for(t in 1:19) { # simulate 20 time steps
  n[t + 1] <- lambda * n[t]
}

最初の集団サイズがないと次がわからないので、n[1] <- 10として10個体からスタートすることを指定。また、集団増加率もlambda <- 1.1としてこちらで指定してあげている。これらがいわゆる「パラメータ」と呼ばれるもので、統計モデリングにおける推定対象になるものだ。シミュレーションでは、これらを任意の値に定めてやることで、例えば「集団増加率\(\lambda\)が1.1ならば、10年後の個体数n[10]はどれくらいになっているだろう？」などのパターンを予測する。先の計算結果を出すと、以下のようになる。

n
##  [1] 10.00000 11.00000 12.10000 13.31000 14.64100 16.10510 17.71561 19.48717
##  [9] 21.43589 23.57948 25.93742 28.53117 31.38428 34.52271 37.97498 41.77248
## [17] 45.94973 50.54470 55.59917 61.15909
x <- 1:20
plot(n ~ x,
     ylab = "Number of individuals",
     xlab = "Time step",
     type = "o")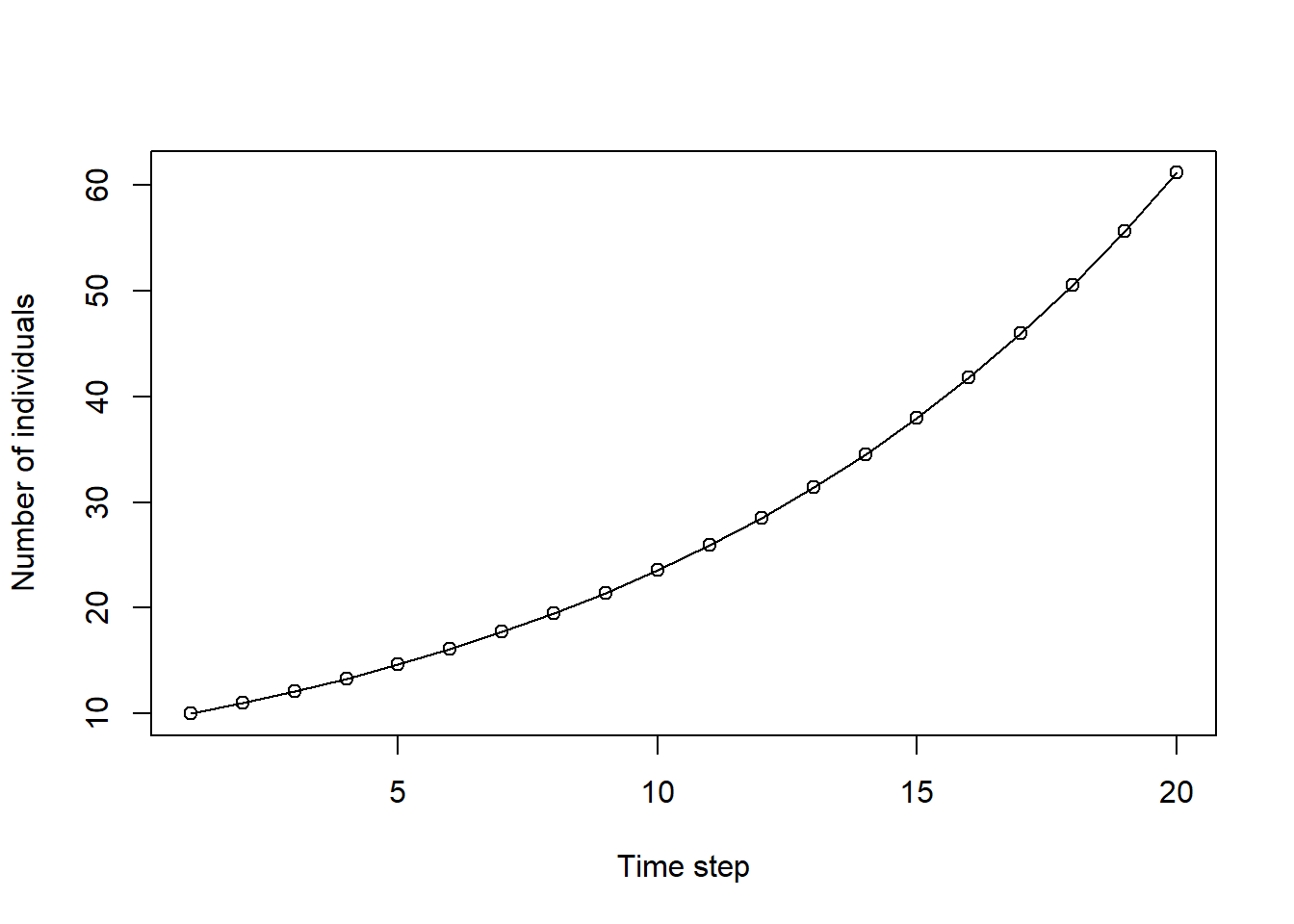

10個体からスタートし、集団増殖率が1.1ならば、10年後の個体数は24くらいになっていそうだ、というのがこの「シミュレーションモデル」にもとづく予測だ。

ランダムネスを加える

先のモデルは「決定論的（Deterministic）」と言われるものである。式が決まっており、そこからの「逸脱」をまったく考えないモデル一般をさす（もっと厳密にいうと、期待値のみをモデル式として表現したもの）。しかし、そうしたことが現実的かというとそうではない。集団の減った増えたに関していえば、たまたま環境がよかった、悪かったなどの理由から、ある年は集団の増加率が1.1を上回ったり下回ったりすることもあるだろう。こうした「ランダムネス」を加えてあげると、より一層現実に即したシミュレーションモデルに近づく。

ランダムネスを表現するには、乱数生成の関数を使う。Rではさまざまな確率分布に基づく乱数生成のための関数が用意されており、それらを使えばランダムネスを比較的容易に表現することができる。例えば、正規分布に従う乱数\(\epsilon\)を考えよう。以下のコードで平均0、標準偏差1に従う正規乱数1000個を瞬時に生み出すことができる。頻度分布を見るとざっくりと正規分布に従っていることがわかる。

eps <- rnorm(n = 1000, mean = 0, sd = 1)

hist(eps)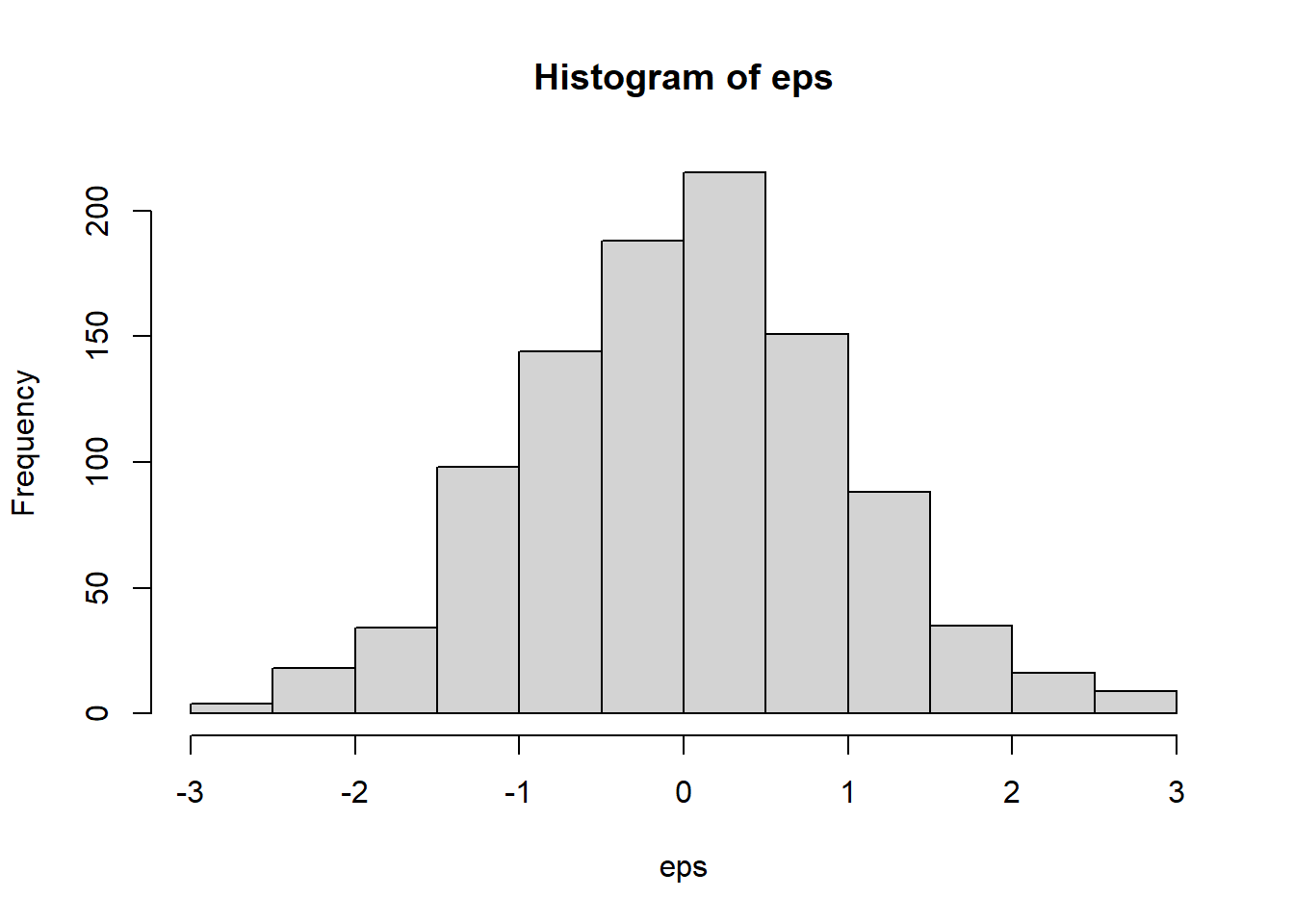

これをシミュレーションモデルに組み込むことで、ジグザグしながら増える集団動態を描くことができる。ただ足し算にすると、負の値をとるかもしれないので（個体数が負の値なのは変）、対数変換したモデル式を考える（元のスケールではすべて正の数になるので）。\(\epsilon\)は標準偏差0.1とする。

\[ ln~n_{t+1} = ln~\lambda + ln~n_t + \epsilon_t\\ \epsilon_t \sim N(0,0.1) \]

# log-transformed population size
log_n <- NULL

# parameters
log_n[1] <- log(10) # initial population size
lambda <- 1.1

# epsilon
eps <- rnorm(n = 20, mean = 0, sd = 0.1)

for(t in 1:19) { # simulate 20 time steps
  log_n[t + 1] <- log(lambda) + log_n[t] + eps[t]
}

# back-transform
n <- exp(log_n)

ランダムネスを加えた場合、こんな感じになる。

x <- 1:20
plot(n ~ x,
     ylab = "Number of individuals",
     xlab = "Time step",
     type = "o")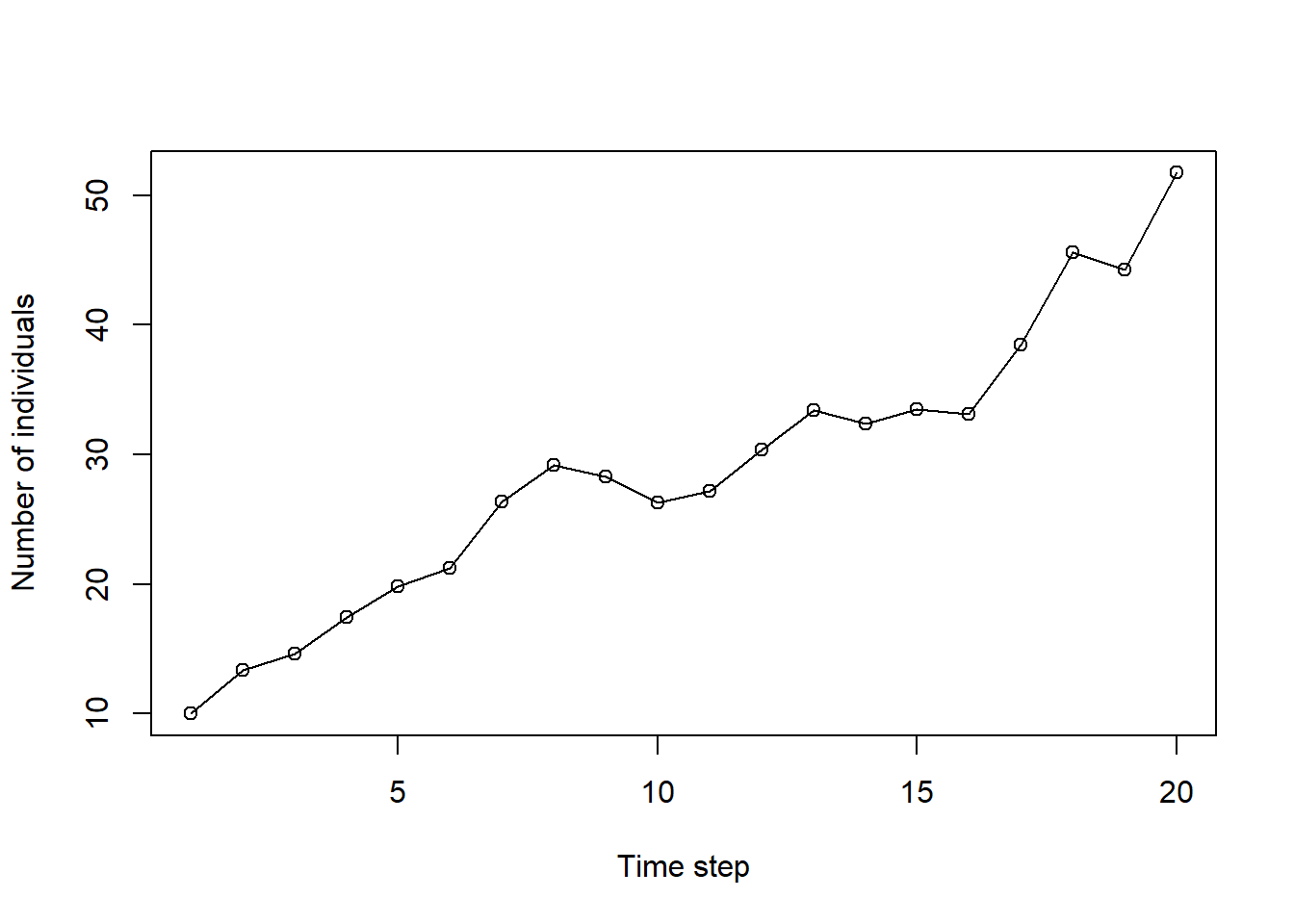

ランダムネスが加わるので、当然結果は毎回ことなる。この理由から、シミュレーションをするときは、同じ条件のもとで100回とか1000回とか繰り返しをとり、その平均的なパターンを見る。

モデルの拡張

今回作ったモデルは非常に単純なので、それなりの数を回しても計算時間が膨大になることはない。しかし、こうした集団が100あり、かつ50種類からなる群集を考え、などとなっていくと、計算量はべき乗的に増え、for構文で素直に繰り返していては永遠に終わらないシミュレーションモデルができてしまう。この問題をいかにクリアするかがプログラムの書き手の腕の見せ所とも言えるかもしれない。気が向いたら空間構造を入れたシミュレーションモデルなんかも紹介したい。