効果量としての標準化偏回帰係数
線形回帰は、生態学の一般的な解析手法になっている。Rで多数の関数が用意されているため解析も容易で、回帰係数の95%信頼区間やp値などでその効果の有意性もカンタンに検討できる。一方、近頃では有意性だけでなく、「効果量(Effect size)」にも注目したほうがいいとの見方が広まっている。この効果量には様々な指標があるけれども、線形回帰の文脈でいえば標準化偏回帰係数がもっとも広く使われている。
そもそも偏回帰係数の意味とは何かというと、対応する説明変数xが単位量(つまり1.0)だけ増えたときに、応答変数がどれだけ変化するかを示している。しかし、説明変数間で単位*1が違うと(例えばある変数はm単位で計られているのに対し、別の変数は㎝単位で計られている)、偏回帰係数はその単位の違いの影響を直に受けてしまう。そこで、それぞれの説明変数をそのばらつき(標準偏差SD)で割り(標準化)、それら標準化された説明変数に対する偏回帰係数を推定する。標準化された説明変数の単位はそろっているので、推定された標準化偏回帰係数も比較できるものになっているはず、というものだ。
しかし、これには一つの問題がある。現代の一般的な統計モデルでは、効果量としての標準化偏回帰係数の解釈が「直感的ではない」のである。例としては以下のようなものがある。個体数のカウントデータを線形モデルで表現する場合、誤差構造としてはポアソン分布(あるいは負の二項分布)を用いることが多い。ポアソン分布の平均パラメータは負の値をとることができないので、Rではデフォルトで対数リンク関数が実装されている。この時、ポアソンモデルの偏回帰係数のなにがどう「直感的」でないのか、下の例を見ながら考えてみる。
まず、下記のスクリプトで簡単な仮想データを作る。
# simulated data
set.seed(111)
n_sample <- 100
x1 <- rnorm(n_sample, mean = 10, sd = 1)
x2 <- rnorm(n_sample, mean = 10, sd = 3)
X <- model.matrix(~ x1 + x2)
b <- c(0.1, 0.2, 0.2) # true parameters
y <- rpois(n_sample, exp(X %*% b)) # simulated yポアソン分布を仮定したGLMを当てはめる。
\[\begin{equation} y_i \sim Pois(\lambda_i)\\ ln \lambda_i = \alpha + \beta_1 x_{1,i} + \beta_2 x_{2,i} \end{equation}\]# model fit; unstandardized
m <- glm(y ~ x1 + x2, family = poisson)
coef(m)## (Intercept) x1 x2
## 0.2210261 0.1902442 0.1991515推定された回帰係数を見ると、真のパラメータを良く推定出来ていることがわかる。ただし、上の例では標準化されていない説明変数をつかっているので、x1とx2の係数の値を直接比較することはできない。そこで、これらの変数を標準化して、もう一度モデルを当てはめる。
# model fit; standardized
m <- glm(y ~ scale(x1) + scale(x2), family = poisson)
coef(m)## (Intercept) scale(x1) scale(x2)
## 4.1024669 0.2037239 0.6089030もともとの偏回帰係数は同程度だったが、標準化するとx2の効果のほうが相対的に大きいことがわかる(x2のSDが大きいため)。
たしかに相対比較はできるけれども、問題はこの回帰係数が対数スケールで推定されている点にある。係数は、「説明変数が単位量変化したときの応答変数の変化量(厳密にはその期待値)」と説明したが、ポアソンモデルでは対数リンク関数を使うので、回帰係数が対数変換された応答変数に対する効果になってしまう。つまり、このモデルで言えば、x1が1.0だけ増えた時、対数変換された\(ln~y\)が0.2だけ増えると解釈しなければならない。別にそれでいいではないか、と思ってしまいがちだが、この問題は実はそうシンプルではない。なぜなら、対数変換は非線形な変数変換のため、x1の変化量は同じでも、起点と終点に応じて元のスケールでの応答変数(つまり個体数)の変化量が変わってしまう(下図)。このため、係数の解釈をする場合に、単純に「x1を単位量だけ増やしたら、個体数はこれだけ増える」とは言えない。
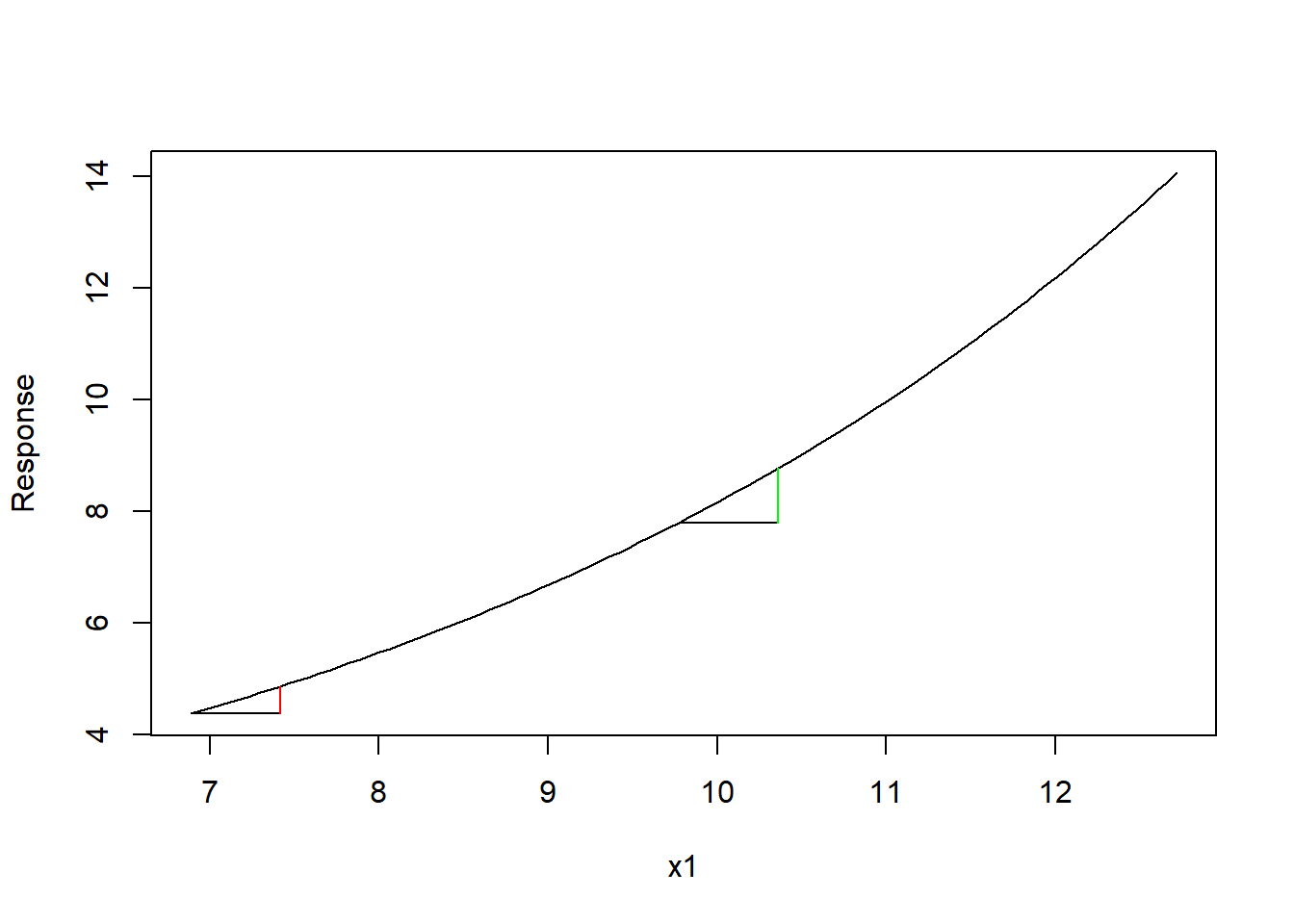
この問題はポアソンモデルに限ったものではない。二項分布を仮定するGLMでは、応答変数をロジット変換するため同様の現象がおきる。また、正規分布のようなリンク関数を用いないモデルであっても、説明変数に交互作用がある場合には同様の問題が生じる。さらに他の共変量の効果もあることを考えるとどうだろう?もう複雑すぎて、とても手に負えたものではない。
Average predictive comparison
これらの問題に対処するため、Gelman and Pardoe (2007)はAverage predictive comparisonと呼ばれる手法を提案している。非線形な変数変換も交互作用もないモデルの場合、この手法の推定値は偏回帰係数と全く同じになる。しかし、この手法では、非線形な変数変換が伴う場合でも、応答変数の元のスケールで各説明変数の効果量が比べられる点に大きなメリットがある。
この手法をGelman and Pardoe (2007)に沿って説明してみる。まず、効果量に興味のある説明変数の値\(u\)とそれ以外説明変数の値\(v\)に分けて考える。まず、ある任意の\(u\)の変化(\(u^{(1)} \to u^{(2)}\))から期待される\(y\)の変化量\(\delta_u\)を求める(basic prediction comparison)。
\[ \delta_u(u^{(1)} \to u^{(2)}, v, \Theta) = \frac{E(y|u^{(2)}, v, \Theta) - E(y|u^{(1)}, v, \Theta)}{u^{(2)} - u^{(1)}} \]
ここで\(E(\cdot)\)は任意の関数(多くの場合、リンク関数の逆関数)、\(\Theta\)は線形モデルのパラメータを示している。しかし、先に述べたように、この変化量は\(u^{(1)}\)および\(u^{(2)}\)、さらには他の説明変数\(v\)の影響ももろに受けてしまう。そこでGelman and Pardoe (2007)はAverage predictive comparisonという量を提案している。
\[ \Delta_u = \frac{\int\int_{u^{(2)}>u^{(1)}}du^{(1)}du^{(2)}\int dv \int d\Theta (E(y|u^{(2)}, v, \Theta) - E(y|u^{(1)}, v, \Theta))~p(u^{(1)}|v)~p(u^{(2)}|v)~p(v)~p(\Theta)} { \int\int_{u^{(2)}>u^{(1)}}du^{(1)}du^{(2)}\int dv \int d\Theta~(u^{(2)} - u^{(1)})~ p(u^{(1)}|v)~p(u^{(2)}|v)~p(v)~p(\Theta) } \]
かなり煩雑な式だが、主な意味は以下の通り。(1)興味のある変数\(u\)の効果をみたいのだが、これはいろんな値をとるのですべての組み合わせについて考えて、その平均をとってやる。(2)ただし、\(\delta_u\)が他の変数\(v\)の影響も受けるので、\(u\)が\(u^{(1)}\)から\(u^{(2)}\)に変わる時に、\(v\)は変化しないという条件付き確率とってあげる。(3)パラメータ推定の不確実性も考えて、その分布の積分をとる(ベイズの場合;頻度主義の場合は推定値とSEから仮想的な確率分布を考えると思われる)。ただ、理論的には正しいのだが、これを有限なデータセットにそのまま適用するのは無理がある。特に\(p(u^{(1)}|v)\)と\(p(u^{(2)}|v)\)を推定できるようなデータセットはまず存在しないだろう(ある二点のデータポイントを考えた時、興味の変数以外が全く同じということはまずありえないので)。代わりに、Gelman and Pardoe (2007)は、以下の近似式を用いてこの量を推定することを提案している。
\[ \hat\Delta_u = \frac{\sum_{i=1}^n \sum_{j=1}^n \sum_{s=1}^S w_{ij}(E(y|u_j, v_i, \Theta_s) - E(y|u_i, v_i, \Theta_s))sign(u_j - u_i)} {\sum_{i=1}^n \sum_{j=1}^n \sum_{s=1}^S w_{ij}(u_j - u_i)sign(u_j - u_i)} \]
ここでは、\(i\)および\(j\)が各データポイントを表しており、それらすべての組み合わせについて和をとることで、\(\int\int_{u^{(2)}>u^{(1)}}du^{(1)}du^{(2)}\)を近似している。\(s\)はパラメータの繰り返しを示しており、ベイズの枠組みで言えば個々のMCMCサンプルが該当するといえば分かりやすいかと思う。この式の肝は\(w_{ij}\)にある。これは\(p(u^{(1)}|v)\)と\(p(u^{(2)}|v)\)を近似するための重み付け関数で、Gelman and Pardoe (2007)はマハラノビス距離にもとづく以下の関数を提案している。
\[ w_{ij} = w(v_i, v_j) = \frac{1}{1 + (v_i - v_j)^T\Omega_v^{-1}(v_i-v_j)} \]
上の式のうち、\((v_i - v_j)^T\Omega_v^{-1}(v_i-v_j)\)の部分がマハラノビス距離の平方に相当する(マハラノビス距離についてはこちらを参照)。この式では、\(v_i\)と\(v_j\)のマハラノビス距離が遠くなるほど、その\(i\)と\(j\)のペアにより小さな重みを与えるようになっている(なお、\(v\)は複数の説明変数からなるベクターであることが一般的なので、多変量空間で共分散を考慮した距離を計るマハラノビス距離を使う)。もともと、「\(v\)は一定のまま、\(u\)は\(u^{(1)}\)から\(u^{(2)}\)に変わる」という状況を考えたい。しかし、実際にそんなデータポイントの組み合わせを見つけるのは難しい。なので、\(u_i\)(このとき\(v = v_i\))から\(u_j\)(このとき\(v = v_j\))になるとき、\(v\)が大きく変化するようなデータポイントの組み合わせには小さな重みを与えよう、という発想なのだ(\(v_i = v_j\)の場合には\(w_{ij} = 1\)となる;Gelmanさん天才)。
実際の計算では、パラメータのMCMCサンプル(ベイズ)あるいは仮想的な確率分布(頻度主義)から得られる繰り返しを考え、次のように計算する。
\[ \hat \Delta_{u} = \frac{1}{S} \sum_{s=1}^S \hat \Delta_{u,s} \]
ここで、\(S\)はパラメータの繰り返しの総数を示す。それぞれのパラメータセット\(s\)についてAverage predictive comparisonを上の式に沿って定義する。
\[ \hat \Delta_{u,s} = \frac{\sum_{i=1}^n \sum_{j=1}^n w_{ij}(E(y|u_j, v_i, \Theta_s) - E(y|u_i, v_i, \Theta_s))sign(u_j - u_i)} {\sum_{i=1}^n \sum_{j=1}^n w_{ij}(u_j - u_i)sign(u_j - u_i)} \]
SEは下記の式から得ることができる。
\[ S.E.(\hat \Delta_{u,s}) = \sqrt{\frac{1}{S-1} \sum_{s=1}^S (\hat \Delta_{u,s} - \hat \Delta_{u})^2} \]
Rで実装
こんな素晴らしい手法、なぜ生態学の界隈で広がっていないのか。どうせRのパッケージくらい誰かが作ってるんだろう。と思い、検索したらなかった。というわけで自分で関数を書いてパッケージ化した*2。まだ試作段階だが、使い方は以下の通り。
以下のスクリプトを実行してパッケージをインストールする。
remotes::install_github("aterui/avpc")今のところ一番ベーシックな関数であるapcompというものしか実装できていない。追って補足的な関数を実装する予定だけど、ひとまずこれで基本的なことはできる。先のポアソンモデルの例をもう一度使うことにする。
# simulated data
set.seed(111)
n_sample <- 100
x1 <- rnorm(n_sample, mean = 10, sd = 1)
x2 <- rnorm(n_sample, mean = 10, sd = 3)
X <- model.matrix(~ x1 + x2)
b <- c(0.1, 0.2, 0.2) # true parameters
y <- rpois(n_sample, exp(X %*% b)) # simulated y
# model fit; unstandardized
m <- glm(y ~ x1 + x2, family = poisson)このとき、モデルの説明変数は標準化しないことを推奨。関数apcompではxが1だけ変化したときのyの変化量をみるので、元の数値の単位が維持されているほうが解釈しやすい(1m増えたら個体数はこれだけ増える;1g増えたら個体数はこれだけ増える、などなど)。このモデルを関数apcompに突っ込み、引数uに興味のある変数を指定するだけ。
library(avpc)
re <- apcomp(m, u = "x1")## the inverse function of log was used to back-transform the response variable y返り値はestimate、sim_estimate、sim_se、df_uv、df_u1v1、df_u2v1、interaction_termがあるが、直接関係あるのは最初の三つ。estimateは線形モデルの点推定値を用いた時のAverage predictive comparison(APC)の値。なので、モデルに相加的な項しかなく、変数変換もない場合、この返り値は偏回帰係数と一致する。sim_estimateは、モデルパラメータの推定値を平均、SEを標準偏差とする正規分布からランダムに1000個引っ張ってきて平均をとったAPCの値(シミュレーションの数は 引数n_simで指定できる)。sim_seはその標準誤差(定義は上述)。
re$estimate## [1] 13.70707re$sim_estimate## [1] 13.99792re$sim_se## [1] 3.091321この関数を使うと、ポアソンモデルを使った場合でも、x1が1増えた時に個体数は14増える!のように言えるので、直感的な効果量の比較が可能になる。applyfamilyの関数などと組み合わせれば、複数の説明変数の項かも一挙に推定できる。
input <- c("x1", "x2")
sapply(input, function(x) apcomp(m, u = x))## the inverse function of log was used to back-transform the response variable y
## the inverse function of log was used to back-transform the response variable y## x1 x2
## estimate 13.70707 13.22086
## sim_estimate 14.12767 13.34761
## sim_se 2.98127 2.333258
## interaction_term NULL NULL
## df_uv tbl_df,9 tbl_df,9
## df_u1v1 tbl_df,3 tbl_df,3
## df_u2v1 tbl_df,3 tbl_df,3今のところモデルクラスlm、lmerMod、rlm、glmにしか対応してないけど、時間のあるときにbrmsなんかにも対応できるようにしたい。
*1厳密にはSD
*2エラーなどあったらぜひhanabi0111 at gmail.com連絡ください。ただし、利用に関して、責任などは一切負えないのでご承知を。